Come temevo questo quiz era troppo contorto e probabilmente frutto di una mia perdita di logica (dovuta al coronovirus, risaputo "tifoso" di Archimede?). Cerchiamo, allora, di riportarlo su binari più seri e comprensibili.
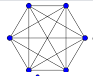
Mi sto sempre di più sforzando di scrivere quiz con domande complesse ma soluzioni molto semplici. Questa volta nessun calcolo, solo pensiero allo stato puro. Un quiz accessibile a tutti.Per chi è ostica la parola grafo, la sostituisca con "figura composta da punti e lati che li collegano". Qui la teoria dei grafi non serve a niente.
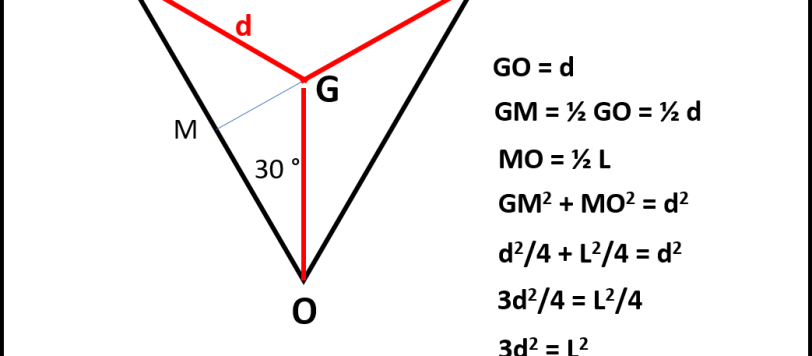
Una formula forse troppo spesso dimenticata che vede una piccola lotta "storica" tra Archimede ed Erone di Alessandria (con qualche infiltrazione cinese). Richiamiamola in quanto può essere di grande aiuto per il quiz sul mostro.
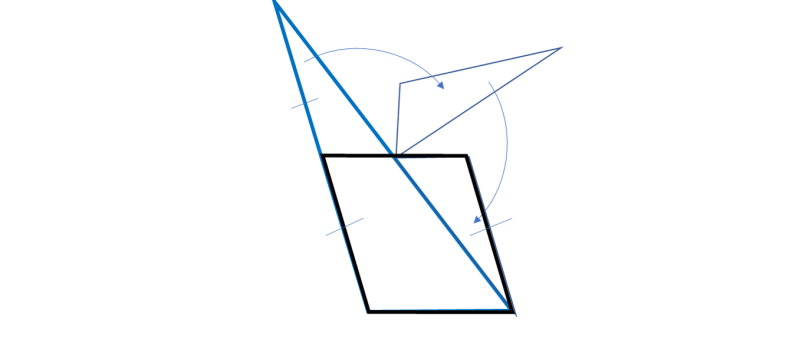
Un esercizio perfetto per chi ama la geometria e detesta l'algebra. Ciò che si deve fare è solo tagliare, ruotare, traslare e incollare ... Un passatempo perfetto per questo periodo di prigionia casalinga e un possibile aiuto per il problema del mostro eroico. Riassumiamolo come dimostrazione di un teorema.
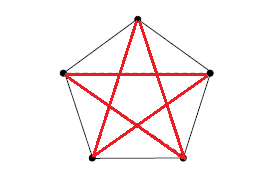
Continuiamo con questi mini-articoli non troppo impegnativi ma che servono anche per distrarci un pò. Proseguiamo verso le teorie di Ramsey con piccoli passi. Passeremo anche attraverso un altro quiz. La matematica discreta è un pò come la teoria degli insiemi; è astratta ma è semplice e affascinante, ed inoltre non richiede prerequisiti matematici profondi […]
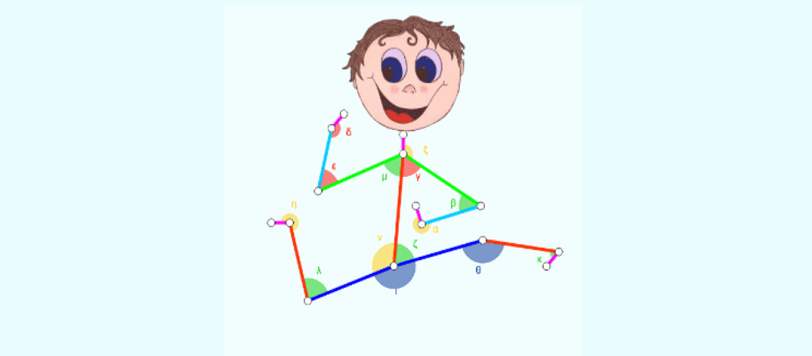
In pieno oceano appare un mostro marino dall'aspetto terrificante. La Scienza non può che analizzare attentamente l'unica fotografia scattata, dalla quale ricava uno schema di massima delle dimensioni e della forma... Chi è che può aiutarci per correre ai ripari?
Vorrei cambiare un po' metodo di stesura degli articoli, e farne tanti di piccole dimensioni , su cose semplici, ma che magari sfuggono alla conoscenza della maggior parte dei lettori. Non mi sono dimenticato della serie su Poincarè, ma l'articolo che sto preparando sulla connessione fra metrica e curvatura è impegnativo, e richiede molto tempo. Introduco questo […]
Un problema che ci avvicina al numero di Nepero (o di Eulero) "e" e che, inoltre, ci permette di richiamare lo studio di una funzione, i limiti e le derivate, nonché un po' di logaritmi naturali.
Una domanda estremamente semplice che necessita di una risposta non altrettanto semplice, anche se alla portata di molti.
Questo articolo va ben oltre il teorema di Tolomeo e introduce una interessantissima trasformazione che si applica al piano euclideo. La sua importanza è enorme in quanto riesce a semplificare molti problemi geometrici, tra cui dare una dimostrazione quasi "ridicola" del teorema di Tolomeo. L'affronteremo solo superficialmente, ma quanto dovrebbe bastare a comprenderne i risvolti più nascosti e generali. Alla fine scriverò una delle mie solite esternazioni e mi aspetto commenti e critiche più che giustificate... Insomma, non perdetevi questo articolo e non consideratelo solo una piccola tessera legata al grande genio di Tolomeo.
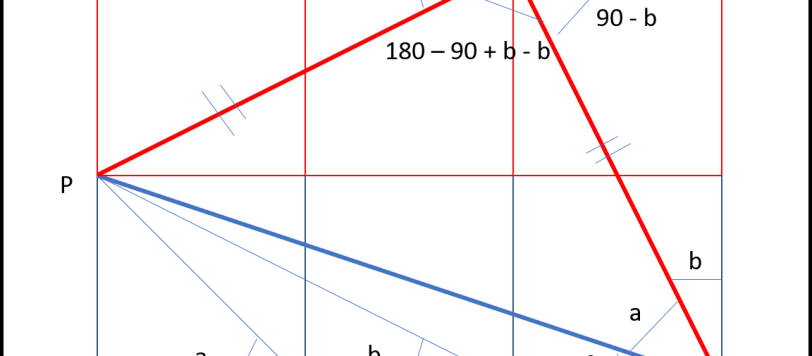
Beh... cari amici, devo dire che il nostro Oreste Pautasso ha cercato veramente di presentarci tutti i 54 metodi di risoluzione della prima parte. Abbiamo dovuto abbatterlo dall'albero su cui si era rifugiato per farlo smettere. Ovviamente, per partito preso e per alto senso democratico, nessuno dei suoi metodi può essere considerato "elegante" come quello che avevo in mente io!
Posso dire di essere molto contento, in quanto quello che desideravo si è avverato; lo scopo era trovare una soluzione alternativa ad un problema molto importante per introdurre la teoria di Ramsey nel piano Euclideo. Ringrazio dunque Vincenzo per essere riuscito in tale intento; il problema non è banale anche se le soluzioni sono semplici. […]
Questo articolo ci mostra come l'applicazione del teorema di Tolomeo porta alla determinazione di due tra le più utilizzate formule di trigonometria.
Un doppio quiz, a due livelli. La prima parte si può risolvere in moltissimi modi. Un prestigioso regalo a chi darà la risposta più "elegante" (a mio giudizio, ovviamente!).
Esiste una classe di affascinanti problemi , nell'ambito del piano o dello spazio, in cui i punti sono contraddistinti da determinate proprietà. Vedremo come questo quesito potrà servire per introdurre una importante classe di problemi di matematica discreta. Tanto per essere originali, assegneremo, ad ogni punto del piano, il metallo di cui è costituito. Diciamo che […]
La geometria, anche quella più semplice, può diventare un vero spettacolo. Soprattutto se c'è di mezzo Tolomeo, grandissimo scienziato, troppo spesso associato solo alla sua visione eliocentrica dell'Universo.