La soluzione è stata più laboriosa del previsto... tuttavia, ringrazio tutti coloro che hanno provato. Il numero 70 girava, ma quasi sempre con un ragionamento non coretto del tutto.


La soluzione è stata più laboriosa del previsto... tuttavia, ringrazio tutti coloro che hanno provato. Il numero 70 girava, ma quasi sempre con un ragionamento non coretto del tutto.
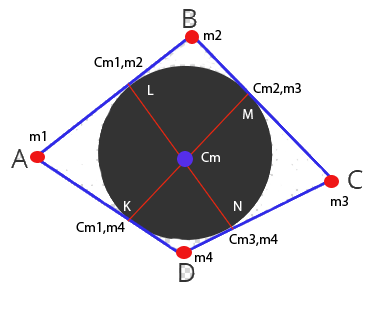
La soluzione da me proposta si basa sulle proprietà del baricentro. Si potrebbe scrivere in modo molto stringato, ma cerco di spiegarla in modo che anche in non esperti in certe proprietà vettoriali del baricentro possano comprenderla. La fisica qui non c'entra niente; lo stesso si avrebbe definendo una certa entità con operazioni da svolgere su vettori con moduli proporzionali a determinati numeri ( numeri detti anche scalari).

Questo quiz di logica più che di matematica è stato letteralmente "sbranato" da Maurizio e nessuno (tranne Ale) ha avuto la voglia di cimentarsi. Cercheremo, la prossima volta, di mettere il bavaglio al nostro Mau... che di questi quiz, relativamente semplici, ne fa un solo boccone!

Un quiz di tanta logica e di poca matematica. Malgrado le apparenze, tutti possono riuscire a risolverlo.
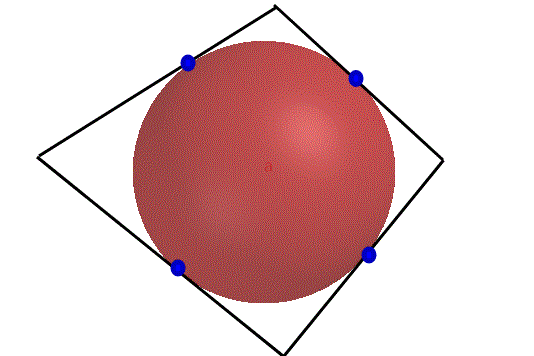
Sto cercando disperatamente di proporre dei quiz che siano risolvibili anche dal cellulare, quindi privi di disegni e calcoli complessi. Lasciamo per un pò perdere poi l'esposizione romanzesca, per essere più precisi, come lo vuole la matematica (anche perchè in questo caso non avrei idee per scriverla). Abbiamo a che fare con una figura sbilenca è una simmetricamente perfetta; cosa succederà ai punti di contatto se si tenta di incastrare una nell'altra?
Un articolo un po' più tecnico dei precedenti, che purtroppo presuppone la conoscenza delle derivate. Tuttavia ciò ci permetterà di sfatare definizioni e formalismi tipici della geometria differenziale, quali i tensori metrici e gli elementi di linea infinitesimi. Ricordiamoci che il nostro scopo è quello di capire come vivere all'interno di una varietà dove di euclideo resta ben poco. In ogni caso, però, tramite il piano tangente possiamo ridurci sempre ad esso.

Questo articolo è estremamente interessante e l'argomento ben poco analizzato (finora almeno). Probabilmente apre un nuovo "mondo" di studi. Leggetelo, quindi, con molta attenzione e mettetevi alla prova. Come forse avrete immaginato, il riferimento al golf non è così forte come si sarebbe potuto credere. Lo scopo era di scuotere un po' il nostro Frank sempre in lotta per scalare posizioni (e anche per prenderci un po' in giro). Che anche lui "scenda" al nostro livello, forse un po' troppo teorico per un tecnogolfista...

Eccovi la mia soluzione che vuole essere un esercizio di fisica (poca) e tanta matematica (in particolare trigonometria). Come già detto, si può probabilmente sveltire il procedimento, ma non è certamente sbagliato.

Qui trovate il quiz e le soluzioni nei commenti. Due parole sulla soluzione, anche se non servirebbe. Intanto la giustificazione dei quattro asterischi per la soluzione completa, ovvero che il percorso indicato dall'autista è quello minimo. Questo era riservato a chi trovasse una soluzione autonoma, indipendente dal teorema di Eulero, che abbiamo visto qui. Nei […]
Un problema di fisica e di matematica a cui ho dato una risposta. Tuttavia, penso che si possa fare ancora meglio, almeno in termini di rapidità. Forza, dateci dentro.... Una bella trota a chi risolverà l'enigma.

Sulla scia dei minimi percorsi, vi propongo questo quiz, più logico però che matematico. Nessun conto da fare, a parte delle somme e delle moltiplicazioni. Quindi aritmetica base . Probabilmente ci sono diversi modi per risolverlo, ma il più elegante riguarda degli argomenti da me trattati in questo sito. Ma chiaramente ogni altra soluzione è ben accettata. Non c'è altro da dire. So che saprete valutare da soli le risposte, mentre il testo penso sia inequivocabile . Buon divertimento!

Questo articolo risponde alla richiesta per la costruzione delle reti autostradali ottimali. Vediamo di fare i vari calcoli e di introdurre un nuovo tipo di percorso minimo.

Parlando di autostrade e di svincoli, mi sembra giusto riproporre questo articolo del 2017, riguardante la vera(?) storia di Napoleone, un genio matematico mai completamente compreso dai posteri. In fondo, è un piccolo aiuto per il nostro problema autostradale...

Lungi da me entrare nelle problematiche dei grafi, sviscerate e trattate con grande profondità dal nostro Umberto. L'intenzione del quiz sulle autostrade è quello di introdurre vari tipi di percorso, assegnando un certo numero di punti da toccare.
Questo articolo-quiz ha un tono scherzoso, dato che era già pronto prima della tragedia. Non voglio cambiare niente e faccio poca fatica a pubblicarlo. In attesa che mi riprenda un po' e che smaltisca le odiose pratiche burocratiche, vi lascio un ricordo in attesa di tempi migliori che DEVONO venire sia per stare dietro a mia figlia, sia perché il tempo a mia disposizione non è tanto... I vostri calcoli e riflessioni a riguardo saranno un angolo di gioia in questo momento così nero. Grazie a tutti. Non so quando riuscirò a rispondere (dipende dai momenti), ma non abbiate timore a commentare e a risolvere... A presto!