Andiamo a vedere come la nostra formica viola ha risolto il problema dello scoglio e si è impossessata del magnifico diamante.
Riporto la soluzione del quiz su Giulietta e Romeo, così come l'hanno scritta un gruppo di lettori.Affrontiamo anche in questo articolo la versione digitale; dei lucchetti matematici e delle chiavi cifrate per scambiare la combinazione di un lucchetto "fisico".
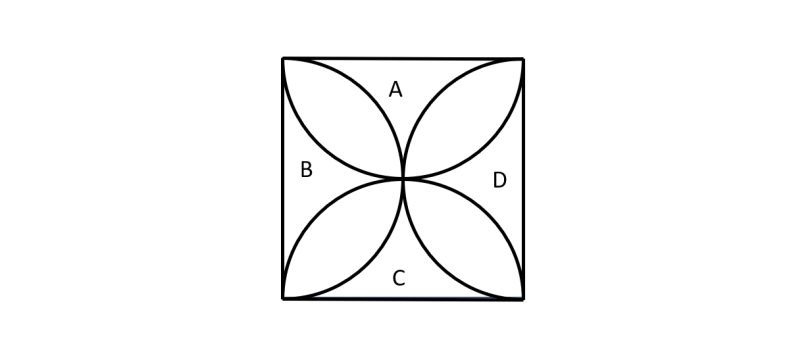
Un semplice problema geometrico ci dà l'occasione di utilizzare un metodo apparentemente più lungo e faticoso, ma di grande interesse per casi molto più complicati. Sconfiniamo nella teoria degli insiemi, ma in modo decisamente elementare.
Una leggenda cosmica che ci permette di risolvere un bel problema di fisica e matematica. Pochi calcoli e un risultato decisamente interessante. L'asterisco in più vale per chi volesse DIMOSTRARE la conclusione.
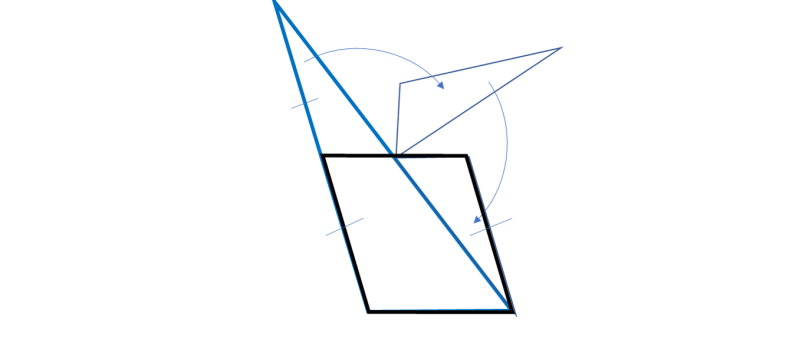
Un esercizio perfetto per chi ama la geometria e detesta l'algebra. Ciò che si deve fare è solo tagliare, ruotare, traslare e incollare ... peccato che nessuno abbia avuto voglia di provarci. Riassumiamolo come dimostrazione di un teorema.
Cosa sarebbe successo a Giulietta e Romeo ai tempi nostri? Forse si sarebbero conosciuti su internet. Un quiz che mi è piaciuto per la sua semplicità, e che propongo pur sapendo che i più esperti possono esserne a conoscenza, essendo un problema classico di logica creativa. Mi auguro che chi lo conosca non partecipi alla discussione. Il problema è si semplice, ma non è detto che la soluzione sia immediata.
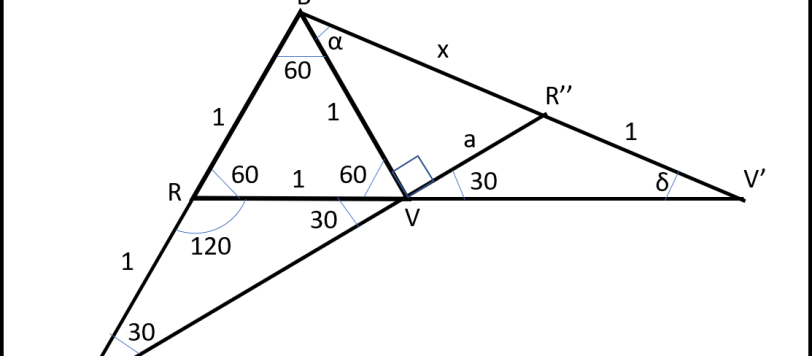
L'esercizio va risolto solo con la trigonometria. Ciò non toglie che alla fine si ottenga un'equazione di quarto grado, la quale, però riesce a essere risolta con estrema facilità. Un bravo a Fabrizio...
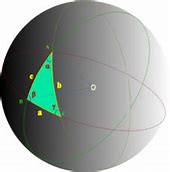
Se vogliamo addentrarci correttamente alla comprensione delle varietà Riemmane, abbiamo bisogno di qualche concetto riguardante argomenti di matematica avanzata, che di solito di studiano nei primi due anni di università . Chiaramente non è nei nostri scopi né nelle nostre possibilità approfondire tali argomenti. Provo perciò a presentarli in modo pratico-intuitivo, sfruttando anche il lavoro fatto da Vincenzo e da Fabrizio. Parleremo di matrici e del loro prodotto, di derivate parziali e equazioni parametriche, nonché di prodotti scalari. Spero che questo sia sufficiente per comprendere uno dei concetti più belli e potenti della matematica che è alla base delle teorie relativistiche e della cosmologia: le varietà Riemmane.
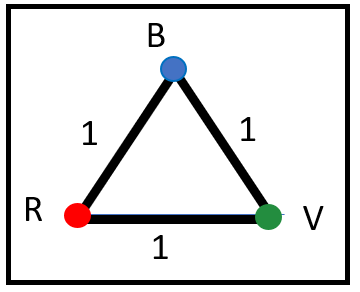
Dopo tanti triangoli abbastanza "imbranati", eccone uno molto preparato i cui vertici si divertono a proporsi, a vicenda, dei problemi non proprio banali. Questo è il regalino di Natale per i più esperti (ma nemmeno troppo, in fondo...).
E' meglio che dia subito la soluzione che avevo in mente, ma che si riferiva solo alle due configurazioni legate ai nostri 41 gatti. Esse avevano entrambe la prima colonna in comune... Fabrizio e Leandro hanno allargato il problema e allora è meglio che crei una pausa. Se poi qualcuno volesse generalizzare ancora di più... sia il benvenuto.
Avevo già preparato l'articolo di risposta, ma siete troppo bravi! E allora, lo lascio a voi come ulteriore esercizio. Niente di veramente difficile, ma è necessario qualche calcoletto...
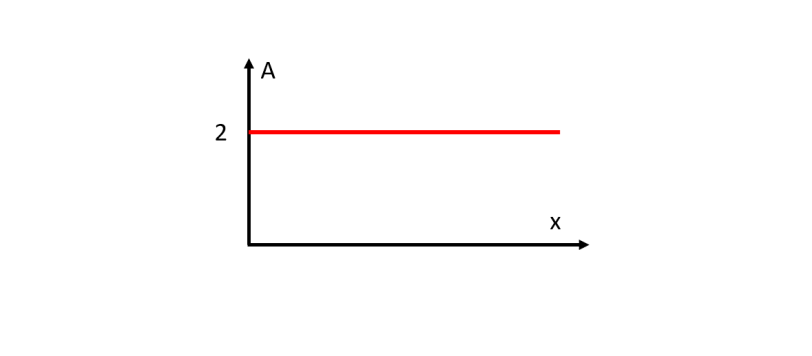
La domanda era poco più che uno scherzo, che Leandro ha subito individuato. Aggiungo la risposta alla domanda di base in modo da ridurre gli spazi...
Un piccolo quiz che ci porterà verso un argomento molto utile per problematiche molto "pratiche". Prima risolvetelo e poi ne parleremo...
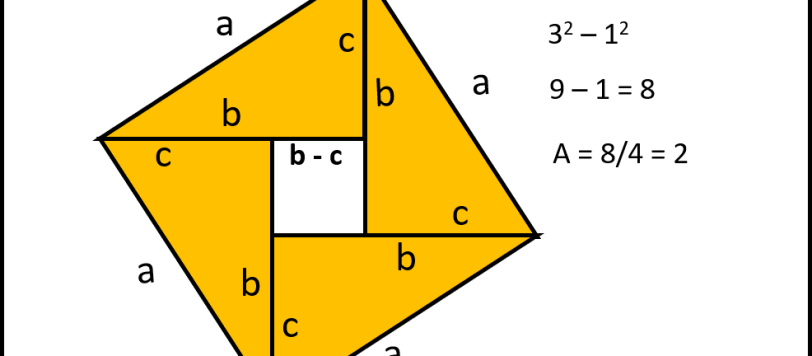
Grazie a Daniele il nostro triangolo è riuscito a calcolare la propria area. Adesso speriamo che prosegua nelle studio delle sue proprietà geometriche che sono tante e strabilianti...
Questo articolo, oltre a dare la soluzione più rapida al problema posto qualche giorno fa, ci mette di fronte a una divertente soluzione seguita da un paio di matematici cinesi che sono riusciti a scalare l'Everest per andare da un villaggio a un altro, uniti da una breve e comoda superstrada... In altre parole: come complicare le cose semplici... Non perdetevelo!
Facciamo divertire anche i meno esperti... Un povero triangolo rettangolo è sicuramente molto intelligente, ma ha appena iniziato lo studio della geometria e della matematica. Gli si fa una domanda che sembra irrisolvibile per la sua limitata preparazione. Riuscite ad aiutarlo?