Un quiz dall'apparenza banale e facilmente risolvibile ha portato a un teorema che nemmeno i greci avevano formulato. Potete fermarvi al livello che volete.
No, non mi sono adattato a una festa puramente consumistica, ma approfitto della data per proporvi un semplicissimo scherzetto matematico (ma è davvero uno scherzetto o c'è qualcosa di più profondo?).
Che gli indiani siano probabilmente i più grandi matematici forse molti lo sanno, ma l'immensità dl genio di Ramanujan è forse troppo poco conosciuto al giorno d'oggi. Parliamone e divertiamoci un po' con le sue scoperte più semplici.
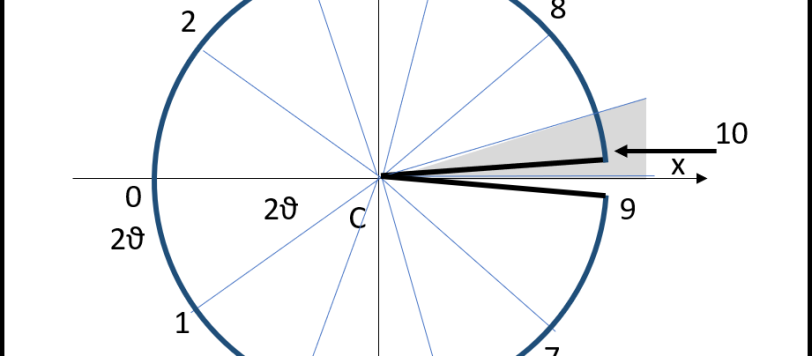
Abbiamo visto che gli urti tra due masse e di una di loro contro una parete riesce a regalarci le cifre significative del pi greco. Analizziamo a fondo il perché, anche se Francesco ha già dato una risposta esauriente. Ci troviamo di fronte a un problema puramente matematico espresso attraverso la meccanica e dimostrabile con la semplice geometria. Un gran bell'esempio di interdisciplinarità.
La prima parte, ossia quella relativa a cosa "saltava fuori" era decisamente facile, anche se molto noiosa...
Nella serie "MATEMATIZZIAMO IL NASTRO DI MÖBIUS", abbiamo visto come generare delle varietà bidimensionali in modo astratto. Riprendiamo in modo meno formale tale procedimento,estendendolo allo studio delle tri-varietà,ossia le varietà di dimensione tre,che non sono rappresentabili nello spazio tridimensionale.
Un esperimento molto interessante che non è certo un vero quiz. Basta usare una fisica estremamente semplice. Tuttavia, per trovare quello che probabilmente non pensereste mai di trovare bisogna o fare tanti calcoli tutti uguali tra loro (poveri noi!) o farsi aiutare da qualche programmino predisposto allo scopo. Penso non sia per niente difficile trovarli già preparati.
Bravi i nostri solutori, anche se il 495 e il 6174 rimangono ancora avvolti nel mistero. Certo è che ancora una volta domina il numero 9.
Questo quiz è decisamente difficile, lo ammetto. Ma in questo Circolo niente è impossibile... Ovviamente è vietata la ricerca sul web, anche se non è facile trovare la risposta...
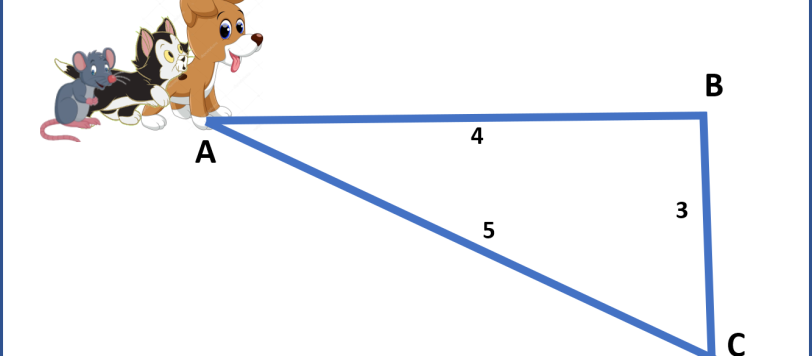
Il problemino sembra subito più difficile di quanto non sia in realtà. Basta ricordarsi che per determinare gli angoli di un triangolo è sufficiente conoscere le dimensioni relative dei lati (come dice Guido).
Un quiz che sembra domandare qualcosa di assurdo. E, invece, anche gli animali sanno fare i calcoli...
Qui trovate il quiz e i commenti. Presento la mia soluzione in modo un po' più formale. Questo per dare una spiegazione in più; già leggendo i commenti di Vincenzo (e anche di altri) si riesce a giustificare la soluzione in modo intuitivo-geometrico.Mi baso su una figura, che è un caso semplificato del nostro problema. […]
Nel 1901 Un lord Inglese,filosofo e matematico,Bertrand Russel, mise in crisi il tentativo di Frege di definire le basi della matematica partendo dalla logica pura, con un paradosso arcinoto a tutti. Tale paradosso era dovuto al fatto che la teoria "ingenua" ovvero intuitiva degli insiemi non era ben fondata. Questo destò grande preoccupazione nel mondo della matematica; se gli insiemi sono alla base della matematica e sono non consistenti, allora tutta la matematica potrebbe essere non consistente, ovvero contraddittoria, e si temette anche per la teoria di Cantor. Ma vediamo perchè successe tutto ciò.Nella realtà attuale, con assiomi consistenti, il paradosso di Russel diventò un teorema.
Ci sono molti modi per costruire graficamente un'ellisse, ma tra i tanti proviamo a trovarne uno che ci permetterà di imitare Newton senza alcuna equazione differenziale. Un quiz che è solo l'ingresso in un mondo straordinario. Chi conosce la storia è pregato di tacere e fare pensare tutti gli altri... grazie!
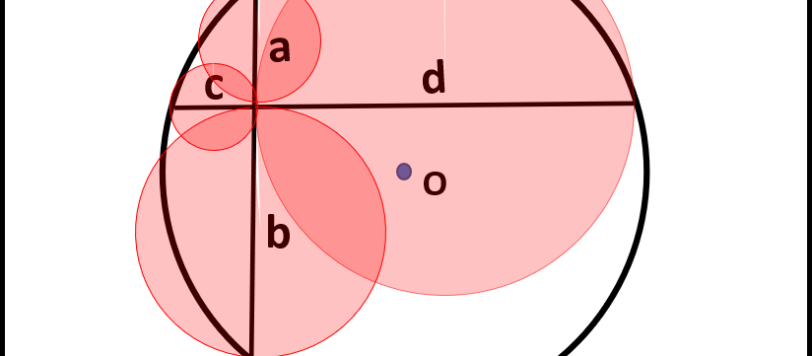
Ecco la soluzione puramente geometrica, anche se, come sempre, il risultato si poteva ottenere in modo analitico.
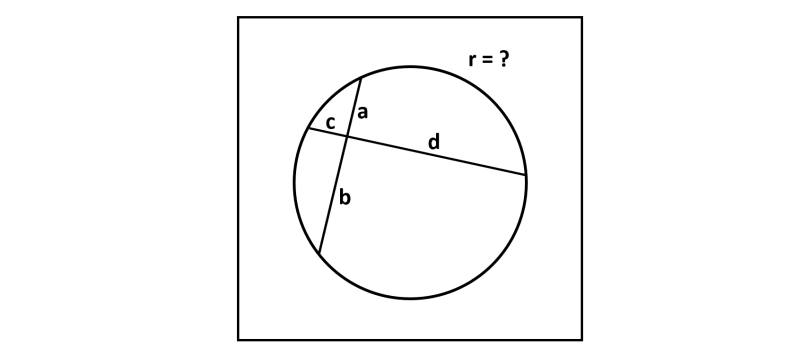
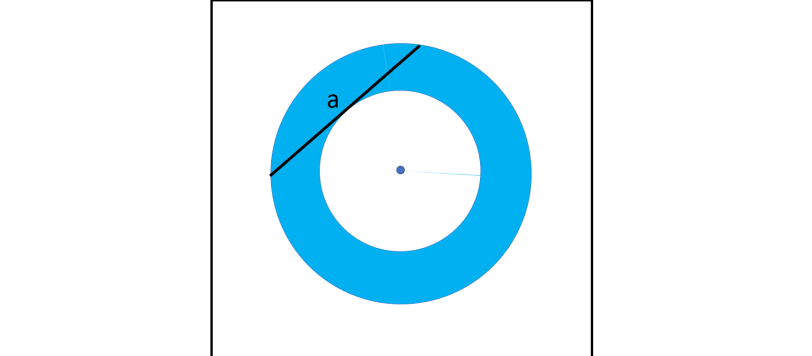
Mentre i più bravi stanno lottando con la molla di Arturo, lasciatemi proporre un semplice (ma non banalissimo) quiz geometrico. Da domani mi prenderò una settimana di ferie rilassanti (soprattutto alla ricerca di funghi) e penso di connettermi poche volte (tutto dipende dai ... funghi). Insomma, ce n'è per tutti i gusti. Prendiamo una bella circonferenza […]