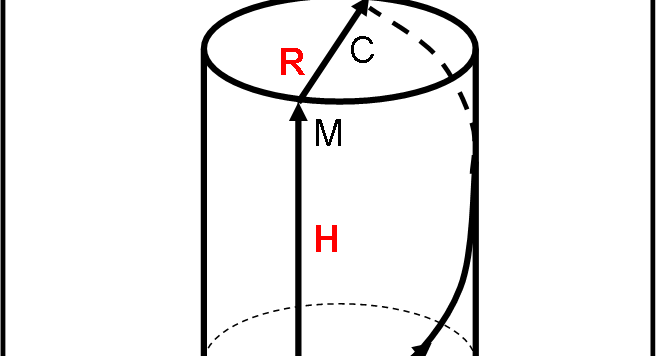
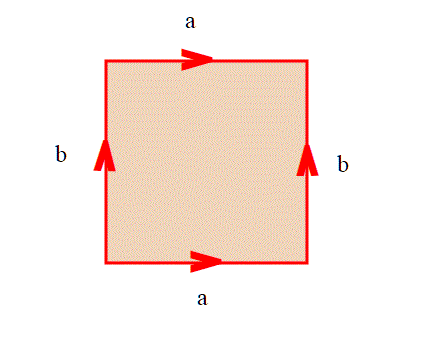
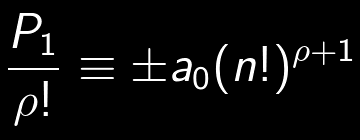Avevamo lasciato la nostra formica in preda ai dubbi che le aveva instillato l'amico scarabeo.
“Stai attenta, cara amica. Tu hai preso una decisione trascurando la logica matematica. Sei arrivata a una conclusione senza valutare veramente tutte le variabili del problema. E’ un po’ come se tu avessi scelto la soluzione basandoti solo sui casi estremi, senza valutare le possibilità intermedie.”
Così l'aveva ammonita, guardandola da sopra i suoi occhialini da presbite (o forse erano multifocali...mah).
Ricordate?
Ebbene la formica non è una che si tira indietro. Occorre studiare tutte le possibili alternative? Benissimo, e che sarà mai ?