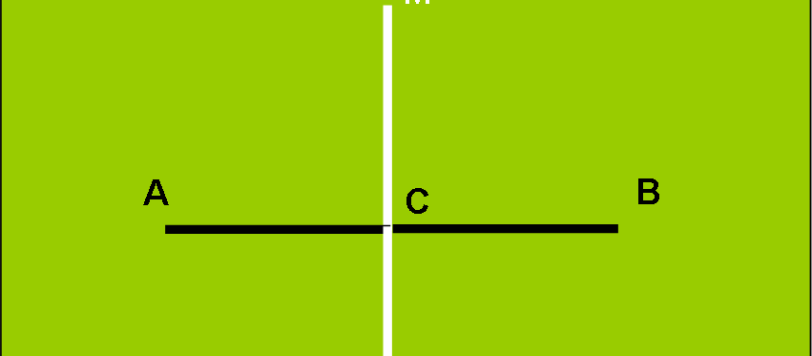
Un quiz matematico-geometrico che potrebbe servire come esercizio in vista dei prossimi esami di maturità. Non un vero problema, ma solo un quesito o poco più…
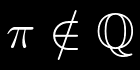
Che π fosse un numero irrazionale, era già stato intuito migliaia di anni fa. Ma la prima vera dimostrazione risale al 1770, ed è dovuta a Johann Heinrich Lambert (1728-1777). Successivamente furono date altre dimostrazioni. Quella che
vedremo sembra attualmente la più semplice ed è stata data nel 1946 da Ivan Niven (1915-1999).
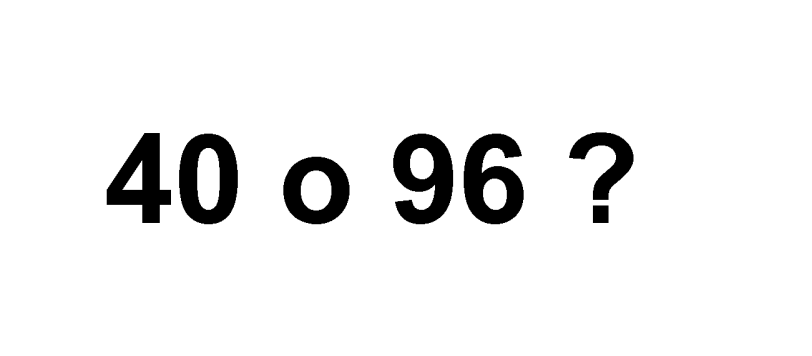
Mi riferisco in particolare al quiz “appendice di whatsapp”, che ha posto un problema di fondo che riguarda la maggior parte di questi problemini che invadono il web e che spesso fanno parte dei test attitudinali e dei concorsi pubblici. Esiste una vera soluzione? E che tipo di soluzione si cerca?
I numeri interi e i loro multipli, interpretati come onde che si propagano verso l'infinito; un modo inconsueto di riflettere sulle proprietà dei numeri interi consecutivi entro un intervallo di valori, il tentativo di capire cosa accade lontano studiando ciò che è vicino. Una specie di surfing sulla cresta delle onde, sul loro affastellarsi, morire e rinascere.
La presenza del quiz di Umberto mi ha spinto a inserire questo nuovo quiz che dimostra in modo molto chiaro ciò che si è discusso nell’altro problema. Va quindi affrontato dopo quello su WhatsApp. Esiste un’unica soluzione? E se ce ne fossero almeno due come fare a scegliere la migliore? E cosa vorrebbe dire “la migliore”?. Insomma, consideriamolo una ovvia appendice del precedente.
Cambiamo un po' stile e andiamo direttamente su WhatsApp.. Un quiz dedicato veramente a tutti (lettori e non) che non abbisogna di nessuna cultura matematica o fisica avanzata. Magari potrebbe essere la strada giusta. Chissà..
Diamo QUATTRO soluzioni per il quiz geometrico sullo strano quadrilatero confinante con il terreno di Nobody. Se ne arrivassero di nuove le aggiungeremo. Per cui guardate bene il “quattro” iniziale, se diventasse cinque o sei sapreste che c’è qualcosa di nuovo da leggere…
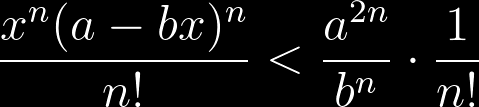
L'idea iniziale era di proporre sotto forma di quiz i prerequisiti necessari per poter comprendere un noto teorema che per ora tengo ancora nascosto. Purtroppo vista la scarsa partecipazione, ho deciso di non proporre l'ultimo quesito e risolverlo direttamente. Non vorrei tediare ulteriormente i lettori che cercano altri tipi di quiz.Ciò non toglie che chi ha in mente una soluzione migliore può scriverla tranquillamente nei commenti.
Ottimo risultato ottenuto dalle nostre “punte” di diamante, abili di mente, ma anche di mano. Forse non lo sanno, ma hanno risolto il problema di un genio islamico dal nome (originale) impronunciabile…
In questo articolo descriviamo più accuratamente il metodo di esaustione e ci dedichiamo a seguire passo passo l’approssimazione del pi greco trovata da Archimede. Una trattazione a livello di scuola media, ma utilissima anche per chi voglia capire veramente come si può arrivare a conclusioni geniali senza algebra e senza trigonometria. Un’immersione completa nella mente del grande siracusano. Riportiamo anche la soluzione della quadratura del cerchio per mezzo della cicloide e un piccolo quiz.
Parlare di Topologia senza parlare di spazi connessi è assurdo. Ho perciò dovuto introdurre due articoli sulla connessione. Poi potremo vedere come matematizzare il nastro, ovvero scoprire cosa significa "incollare" in senso matematico.
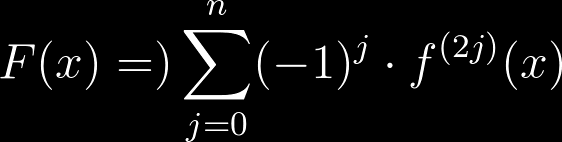
Continuiamo con questi mini-quesiti che una volta messi assieme comporranno la dimostrazione di un famoso teorema nell'ambito della teoria dei numeri. Vi prometto che siamo quasi alla fine, potrebbe essere la penultima puntata. Questo miniquiz è un po' più facile dei precedenti, ma è essenziale per risolvere l'obiettivo finale, che per ora tengo ancora nascosto.
Pippo, Pappo e Peppa si sono comprati degli appezzamenti di terreno per costruirsi tre casette separate. Purtroppo, la forma totale ABECD non è certo l’ideale per essere diviso equamente.
Achille ha fatto la scelta giusta, rinunciando a sfidare la Tartaruga per avere la rivincita , l'ipotesi di scendere lungo il piano inclinato nella speranza di impiegare meno tempo di quello della tartaruga, lungo la cicloide, era assolutamente da scartare.
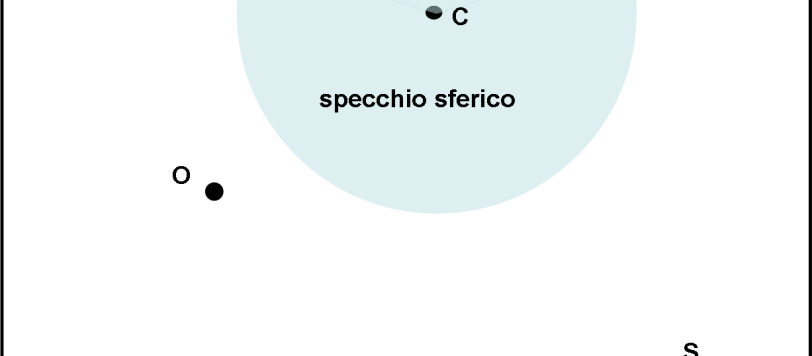
Basta con equazioni, numeri, funzioni, trigonometria, algebra, geometria analitica… è arrivata l’ora di “sporcarci le mani”, come facevano i grandi geni dell’antica grecia e non solo. Eccoci di fronte a un problema da risolvere "meccanicamente" e -magari- costruire con le proprie mani.
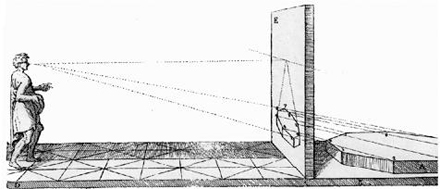
Riportiamo la soluzione, già largamente compresa da alcuni lettori, e spieghiamo perché solo uno dei tre amici è riuscito a risolverlo. Non poteva che essere Pappo, dato che tutto si collega al suo teorema… Il quiz è solo un inizio che ci porterà verso la geometria proiettiva e la sua fondamentale importanza nella storia dell’arte.