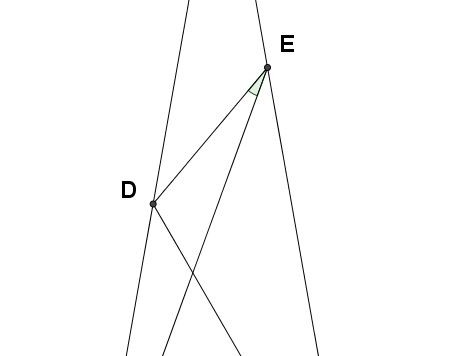
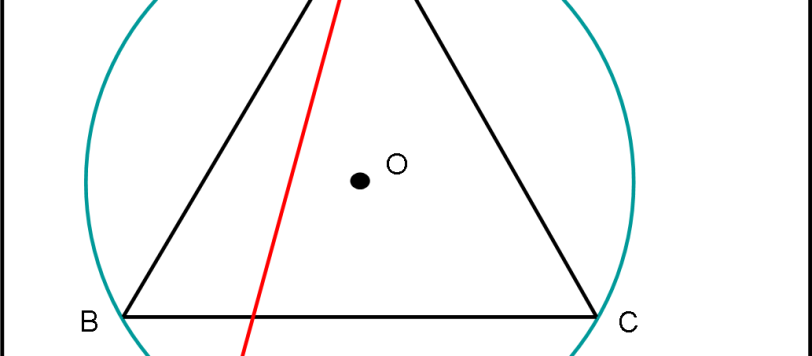
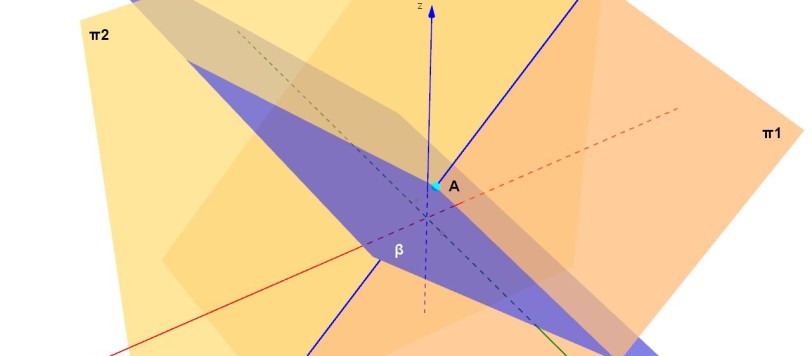
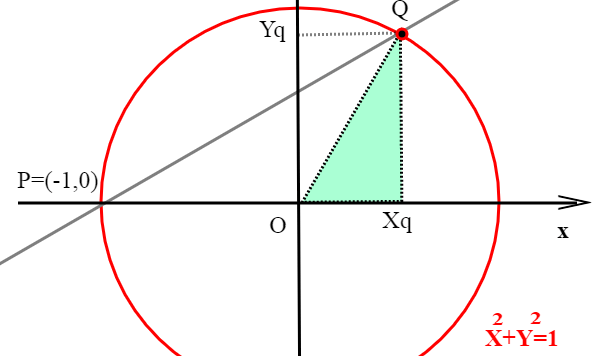
Vi proponiamo un quiz di geometria piana che ha attirato la nostra attenzione perché si presta ad essere risolto seguendo strade diverse. Anche stavolta ve lo proponiamo per mezzo del nostro simpatico amico Oreste. Eccovi la lettera che ci ha fatto pervenire...
IN CALCE AL QUIZ UN SUGGERIMENTO INSERITO IL 27/2/2017
Per analizzare correttamente le equazioni algebriche sotto nuovi punti di vista (tipo quelle ellittiche usate da Wiles per la dimostrazione della congettura di Fermat) bisogna avere a disposizione una nuova struttura algebrica: il Campo. Nell'immagine Euclide; i suoi algoritmi sono ancora attuali perfino nelle moderne congetture matematiche.
Iniziamo dal caso più facile, introdotto con l’aggiornamento del quiz in data 4-febbraio-2017, ossia il caso in cui gli interi possibili sono soltanto quelli tra 1 e 9. Le eventuali quaterne di numeri che soddisfino la condizione del quiz sono da ricercare tra le combinazioni di 9 numeri (da 1 a 9) presi a 4 […]
Il quiz sul triangolo si risolve immediatamente ricordando un teorema molto antico. Non lo dico nella presentazione per non influenzare chi cerca ancora di risolverlo in qualche altro modo. Va comunque detto che i nostri maghi sono stati più che bravi… Aggiungiamo qualche considerazione su come questo esercizio permetta di trovare graficamente ed elegantemente una formula fondamentale della trigonometria e su come le tabelle trigonometriche, largamente in uso prima dell’avvento dei computer moderni, si poggino su questa relazione.
Non vorrei sembrare troppo arrogante… ma, questa volta, l’apprendista stregone cerca di sfidare il club dei maghi (ma non solo loro). Abbiamo bisogno soltanto di una circonferenza e di un triangolo equilatero. I procedimenti per ottenere la soluzione sono molti e quindi potrebbe diventare un vero "tormentone", come già successo per altri quiz.
Qual'è la cardinalità del piano? A occhio e croce ben di più di quella della retta, che ha cardinalità c, pari dunque a quella dei numeri reali. Invece avremo una gran bella sorpresa: la cardinalità del piano è uguale a quella della retta. Questo fatto è fortemente controintuitivo. Lo stesso Cantor , in una lettera a Dedekind ,dove ne riporta la dimostrazione, scrive: "Lo vedo, ma non lo credo".
AGGIORNAMENTO 4-2-2017 a fine articolo
E' con grande piacere che il Club dei Maghi accoglie tra le sue fila l'amico Mauritius, già ben conosciuto nel Circolo come scrittore di racconti, riflessioni e poesie. E' per questo, cari lettori, che noterete un certo cambiamento di stile nella stesura del testo dei quiz. Ma non preoccupatevi, gli incorruttibili matematici circolari lo terranno sotto stretta sorveglianza (poveri loro...) e non permetteranno che si prenda licenze poetiche sulla correttezza formale dei quesiti proposti! Perché qui si ride e ci si diverte, ma guai a scherzare sui quiz!!
Questo articolo è adatto a tutti, in particolar modo ai bambini che sprizzano fantasia da tutti i pori. Partiamo da una farfalla e ci accorgiamo che la geometria ci porta quasi automaticamente a spiegare alcuni tra gli oggetti più misteriosi e affascinanti del Cosmo. L'articolo era già apparso molto tempo fa, ma ho giudicato interessante riproporlo dato che con oltre 1800 articoli, i nuovi arrivati (e sono tanti) potrebbero trovare difficoltà a trovarlo nell'archivio... Se la cosa piacerà, ogni tanto faremo lo stesso con altri articoli particolarmente stimolanti e sempre attuali.
Nel precedente articolo, che potete rileggere QUI, ho introdotto il concetto di parametri direttori di una retta nel piano. In questo estendiamo il concetto alla retta nello spazio e al piano. Passiamo, quindi, nel riferimento cartesiano dello spazio.
Come tutti avranno capito , la parte iniziale del quiz che trovate QUI non ha soluzione, ovvero per n>2 non è possibile trovare degli interi a,b,c tali che: per n>2 e che altro non costituisce che l'ultimo teorema di Fermat, Useremo la sigla UTF per indicare tale teorema; in realtà sarebbe più corretto chiamarlo teorema di Wiles, […]
Il viaggio verso l'equazione di Eulero-Lagrange continua.
Occorre fare ancora una tappa per completare la conoscenza delle derivate utilizzate nella equazione.
Come nei gruppi ben affiatati che affrontano i sentieri di montagna, procediamo ad un passo che spero possa permettere a tutti di godere del percorso.
Il quiz era estremamente semplice e penso sia stato risolto da molti, anche se non hanno fatto sentire la loro voce. In poche parole, bastava descrivere il “crivello di Eratostene”, una specie di setaccio (crivello, appunto…).
In questo articolo e in quello successivo intendo illustrare un elemento sinora da me mai citato ma che , come vedremo, si rivela molto utile nella trattazione di problemi di geometria, in particolare quella dello spazio. Tale elemento caratterizza una retta, indicandone la direzione, oppure un piano, consentendoci di individuarne subito tutte le infinite rette ad esso perpendicolari. Scopriremo che sia la retta sia il piano si "portano dietro" questo elemento come una targa identificativa, che a noi basta quasi leggere per conoscere subito, in termini analitici, la direzione della retta o la giacitura del piano.
Abbiamo visto numeri difettivi e numeri eccedenti, ciascuno con i suoi problemi esistenziali. I loro stessi nomi indicano chiaramente che devono esistere anche dei numeri perfetti, ossia tali che la somma dei loro divisori sia esattamente uguale al numero. E si apre un argomento ancora oggi non risolto del tutto…
Cari amici terricoli,
se qualcuno pensava di essersi liberato di me, mi dispiace deluderlo ma, più mi guardo in giro, più il vostro pianeta mi piace e ho intenzione di conoscerlo molto bene prima di tornare nel mio! Come qualcuno di voi avrà già capito, sono Quazel l’alieno e, grazie al prezioso aiuto di PapalScherzone che riesce a comprendere e a tradurre il mio linguaggio, sto per proporvi un nuovo quiz!
L'equazione di Eulero-Lagrange richiede che siano fatte alcune derivate della lagrangiana.
A prima vista queste derivate hanno un aspetto che potrebbe intimorire, ma dietro l'apparenza non c'è niente di particolarmente difficile rispetto a quelle viste negli articoli di Enzo. Occorre solo farci l'abitudine.
Per iniziare a familiarizzare con queste derivate ho pensato di proporvi questo percorso di avvicinamento alla equazione di Eulero-Lagrange. Strada facendo faremo l'abitudine ad uno degli aspetti che a me ha inizialmente confuso.