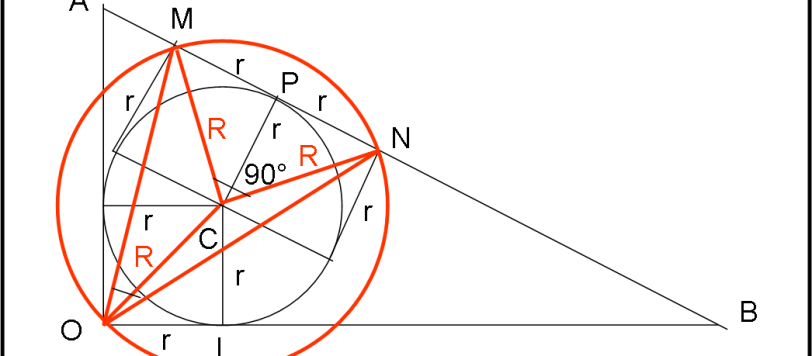
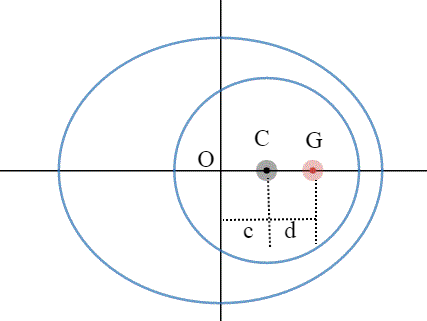
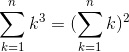Il mio tentativo di “incastrare” i più bravi, proponendo uno studio di funzione, quando il tutto è risolvibile con semplici considerazioni geometriche, è fallito miseramente e … ne sono contento! Sono, inoltre, particolarmente grato ad Arturo che, pur capendo l’inghippo, si è cimentato, comunque, nello studio analitico (in due modi), ottenendo, ovviamente, la soluzione geometrica. Propongo direttamente i suoi manoscritti come ottimo esempio di trattazione matematica (anche se praticamente inutile). Lo so, faccio troppi complimenti ad Arturo… ma quando ci vuole, ci vuole… Complimenti anche a Gimar e Leandro, ovviamente…