Questo è un quiz matematico veramente carino e semplice, adatto anche a chi ha frequentato soltanto le scuole secondarie di primo grado. Per l’ultima parte, invece, ci vuole qualcosina in più.
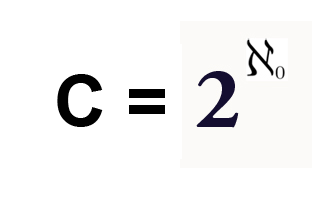
Ci stupiamo ancora una volta di come l'assioma di continuità e una sua importante conseguenza (l'assioma di Archimede) , svolgano una parte essenziale nelle dimostrazioni riguardanti la cardinalità di R.
Questa puntata è estremamente corta e anche molto facile. Anche la terza formula fondamentale si ottiene partendo dalla prima e giocando un po’ con la matematica (roba da poco).
La seconda formula fondamentale è sicuramente la più “difficile” da ottenere. Non spaventatevi, però… sono solo passaggi matematici alla portata di tutti. Inoltre, si può notare come piccoli “trucchi” possano rendere la matematica estremamente intrigante e utilissima per mettere alla prova la nostra capacità di seguire ragionamenti logici di importanza ben più generale.
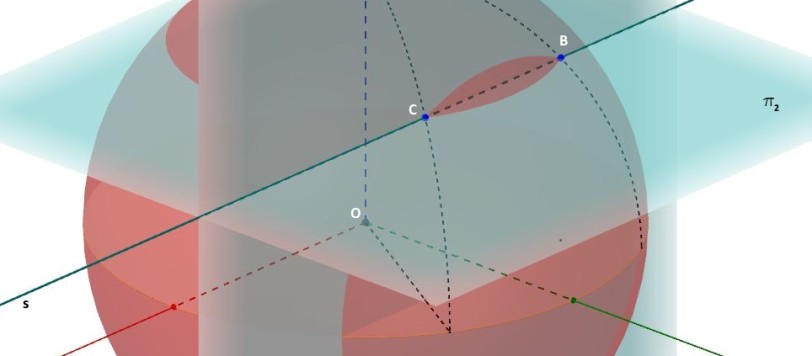
Dopo il primo articolo sulla geometria solida, pubblicato in due parti QUI e QUI nelle scorse settimane, eccoci ora giunti a questa appendice. In essa, mettendo in pratica i concetti di geometria solida sinora esposti, con particolare riferimento al piano, al fascio proprio di piani e alla sfera, dimostreremo che, dati due punti su una […]
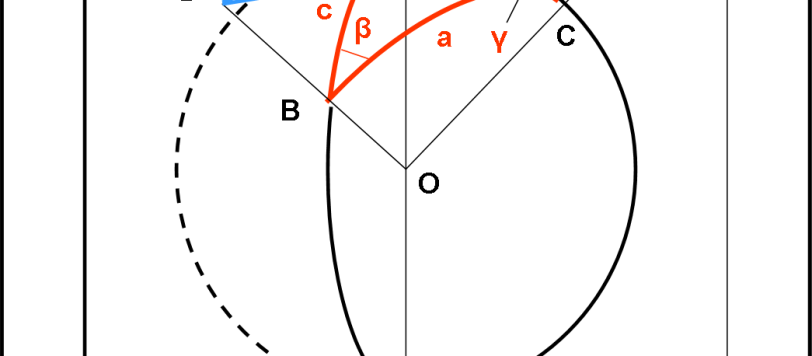
Definito il triangolo sferico, sia intrinsecamente che estrinsecamente, non ci resta che determinare alcune formule fondamentali che leghino tra loro i lati e gli angoli. Esse vengono proprio chiamate le tre formule fondamentali della trigonometria sferica.
L'insieme di Cantor, anche detto polvere di Cantor, ci servirà per provare che la cardinalità dell'insieme delle parti è minore o uguale a quella del continuo (R).L'insieme è anche un primo approccio al mondo fantastico dei frattali; nella figura una versione tridimensionale dell'insieme di Cantor.
Attraverso tanti calcoli analitici (di media difficoltà, anche se un po' noiosi) si possono ricavare le tre leggi di Keplero partendo dalla legge di gravitazione universale di Newton. Vi è un solo punto critico relativo alla derivazione della traiettoria del corpo orbitante: un'equazione differenziale che comporta il calcolo di un integrale non banale (per noi almeno). Solo in questo caso accettiamo di prendere un risultato per buono... Per dirla in altre parole, risolviamo un problema fondamentale di Meccanica Celeste: il problema dei due corpi.
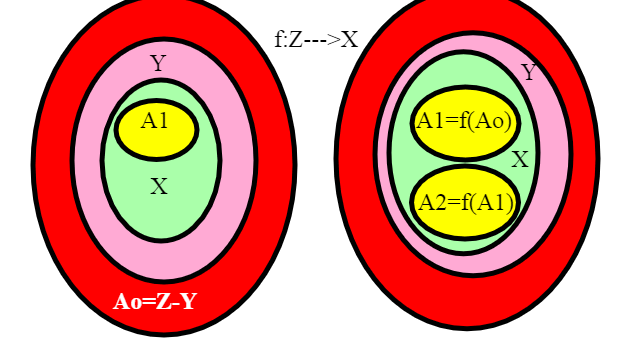
Il teorema di Bernstein risulta necessario per affinare il confronto fra i numeri Cardinali, ed è uno dei teoremi più importanti della teoria degli insiemi.La dimostrazione è complessa ma non estremamente difficile, Vedremo come il concetto di ricorsione, già applicato in altri contesti, occupi una parte dominante nella dimostrazione.
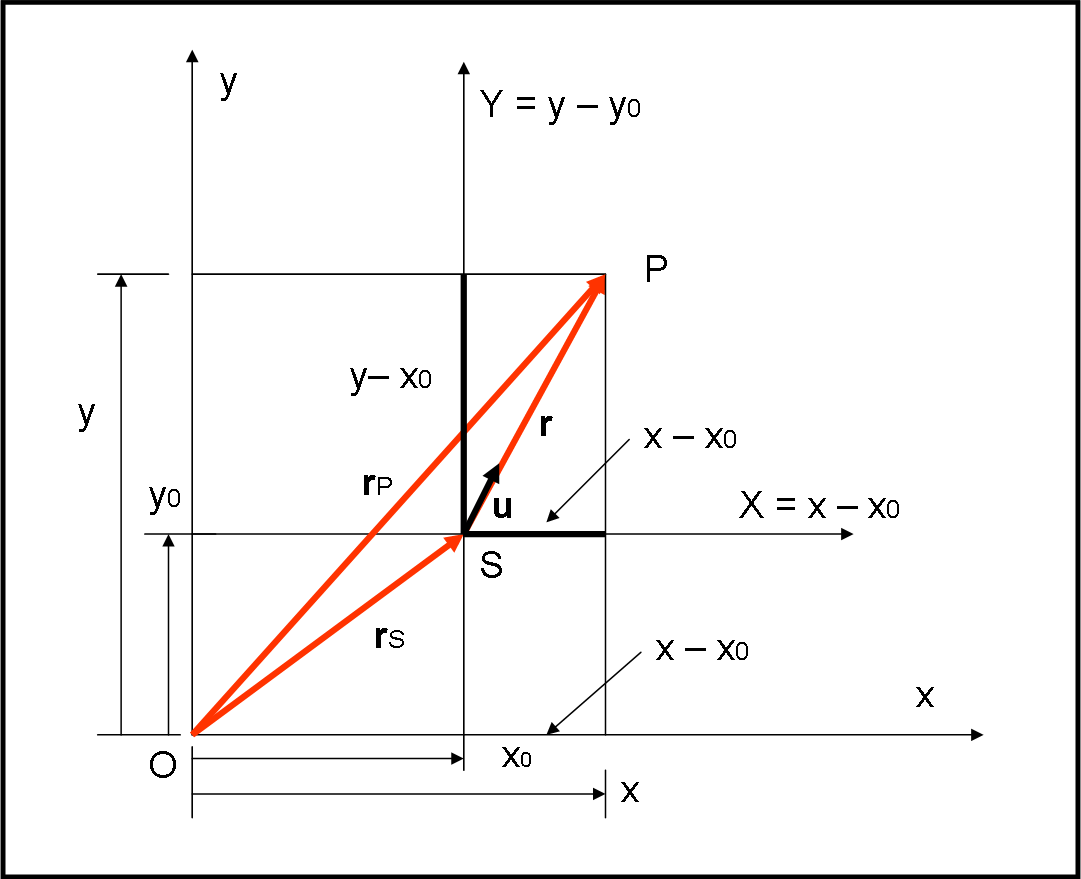
Proseguiamo il nostro percorso nella geometria dello spazio con la seconda parte dell'articolo. La numerazione delle figure e delle formule segue quella della prima parte dell'articolo, che trovate QUI. Fasci di rette nel piano e fasci di piani nello spazio Nel piano le rette posso essere tra loro incidenti, quando hanno un punto in […]
La volta scorsa i papallini in visita al Pianeta dei Numeri si erano imbattuti in un gioco, o meglio un'operazione (come la chiamano i Numeri), apparentemente non risolvibile, ma è davvero così?
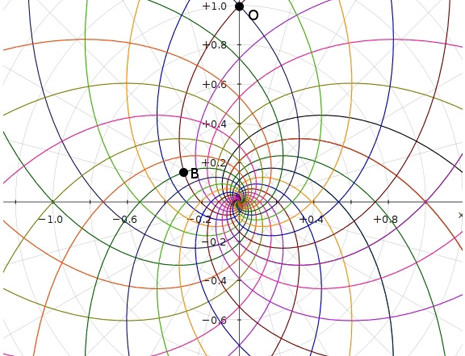
I numeri di Fibonacci restano ancora un meraviglioso mistero. E’ indubbio, però, che la Natura sembra conoscerli molto bene. E forse molto di più di quanto immaginiamo.
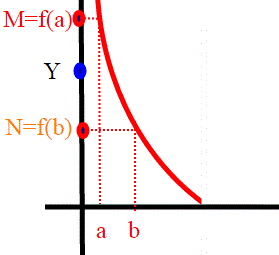
In questo articolo dimostreremo che R non è un insieme numerabile. La dimostrazione sarà quasi immediata servendoci dei risultati dell'articolo precedente, sulle conseguenze della continuità di R. Per giustificare il fatto che ogni intervallo di R è equipotente ad un suo intervallo, ho dovuto rifarmi a importanti teoremi di analisi matematica, di cui però ho dato la dimostrazione in appendice.
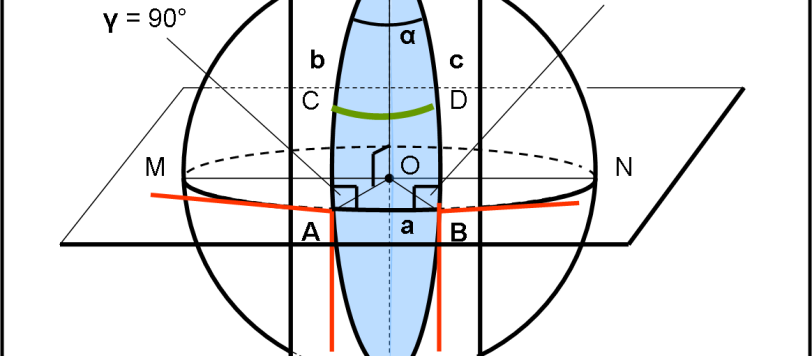
Definiti i lati di un triangolo sferico, non ci resta che definire quali siano i suoi angoli. Nel fare questo, risolviamo il vecchio quiz e stabiliamo anche un’altra proprietà molto interessante dei triangoli sferici. Concludiamo con due nuovi quiz, che saranno risolti la volta successiva.
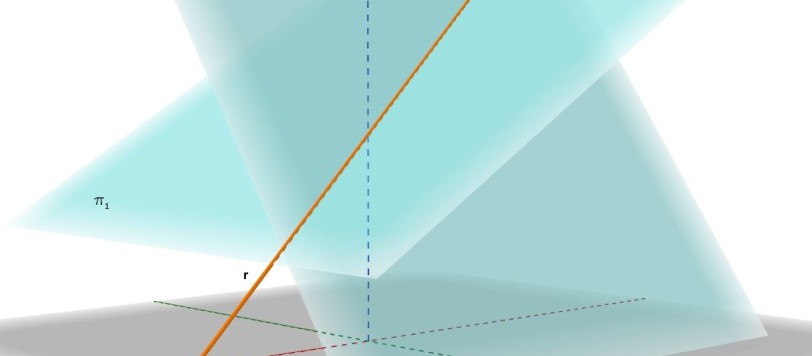
Obiettivo di questo articolo, di cui viene pubblicata ora la prima parte, è quello di entrare nell'affascinante mondo della geometria dello spazio e, dopo la seconda parte, dimostrare che la curva congiungente due punti situati su una superficie sferica e che misuri la minore distanza tra essi è un arco di circonferenza massima, ossia avente centro coincidente con quello della sfera.
Certamente SI risponderebbero i papalliani in coro, niente numeri niente giochi!