Qual'è la cardinalità di N x N? Ad occhio e croce dovrebbe essere maggiore di quella di N. In questo articolo scopriremo invece che anche N x N è numerabile; questo fatto ci spianerà la strada per analizzare la cardinalità di Q, insieme dei numeri razionali.

....Eh si PapalCaronte ha sicuramente il suo fascino come traghettatore, ma in fin dei conti è meno misterioso di quanto vorrebbe far credere... Oggi PapalCaronte è particolarmente socievole, per cui ha deciso di svelare perchè durante il trasporto i denominatori si trasformano in numeratori. …e perchè i numeratori si trasformano in denominatori... PapalCaronte, però, sa […]
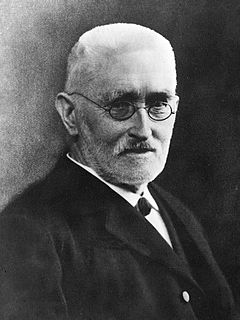
Dopo alcuni prerequisiti essenziali finalmente stiamo cominciando ad intraprendere il nostro viaggio nel Paradiso di Cantor, quello degli insiemi infiniti: gli insiemi numerabili.

PapalPotenza e PapalEstrattore sono alcuni dei nuovi personaggi che animeranno la matematica di Papalla.... nuovi racconti, nuovi personaggi, nuovi giochi...
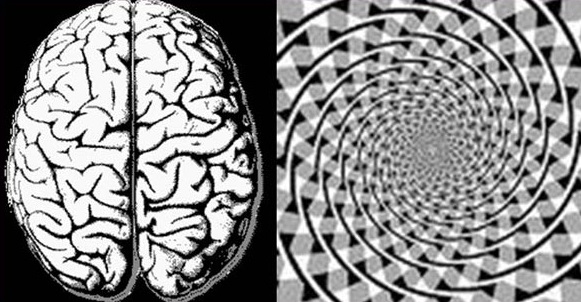
Saranno sufficienti formule iper-algebriche, matematica astrimmaginaria, equazioni differenziali ultrairrazionali e bioalgebra periodica a controllare il caos del cervello umano e della Natura e trasformare la nostra Terra in un'oasi di serenità?
Tra i vari racconti di Vin-Census, oggi ho scelto di riproporre questo, centrato su Intelligenza e Matematica, argomenti del momento. E gli spunti di riflessione non mancano...
La Matematica sta acquistando sempre più importanza nel nostro Circolo, grazie non solo al nostro PapalEnzo (che, con le sue lezioni di Matematica, è riuscito a far comprendere gli integrali anche a PapalSempliciotto!), ma anche ad amici come Paolo e Umberto che, con grande passione, si stanno impegnando per far sì che il maggior numero di persone possibile superi la diffidenza verso questa materia, magari facendoli divertire oppure aprendo loro nuove porte da cui entrare.
Ma a cosa serve la Matematica? E’ una scoperta o un’ invenzione? Come si è arrivati a sviluppare il concetto di numero? In occasione della prossima pubblicazione dei primi articoli dedicati alla Matematica di Papalla, ho deciso di rivolgere tali domande ad uno dei più saggi tra i papalliani, il mio amico PapalMatematico.
L’ho incontrato al bar di Papalla e, tra un succo di limone e una granita alla fragola, abbiamo fatto una bella e piacevole chiacchierata… e non poteva essere altrimenti: è sempre un’esperienza emozionante conversare con chi ha nello sguardo la consapevolezza di parlare lo stesso linguaggio dell’Universo e nel sorriso la gioia di comunicarlo a chi ha la volontà di comprenderlo.
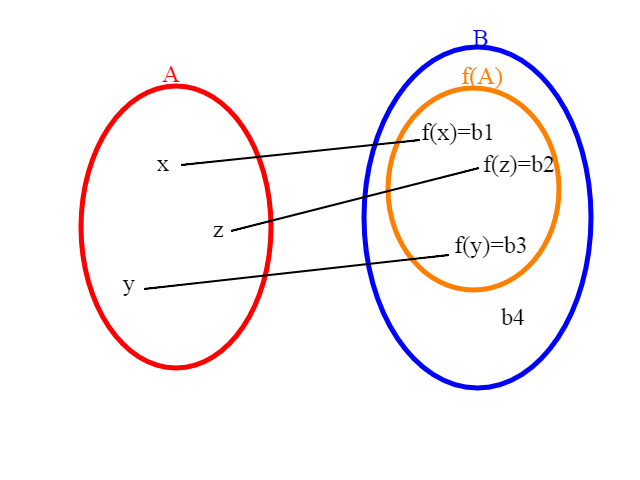
Tutti sappiamo come calcolare il numero di elementi di un insieme finito; basta contarli. E tutti più o meno sanno cosa sia un insieme infinito; ma gli infiniti sono tutti uguali? Lo scopo di questa serie di articoli sarà proprio questo, dimostrare che non sono tutti uguali.
Stiamo parlando molto di matematica, a tutti i livelli. Normalmente si associano grandi capacità di pensiero a grandi capacità di sintesi matematica degli stessi pensieri. In generale, l’intuizione matematica è uno degli indici usati per misurare l’intelligenza o almeno un certo tipo di intelligenza. E allora, lasciatemi ripensare a cosa sia l’intelligenza e se la deduzione un po’ teologica e un po’ egoistica dell’uomo come unico possessore di questa potenzialità mentale non sia tutta da rivedere. Ho intenzione di tornare sull’argomento, attraverso recenti studi scientifici… per adesso mi limito a riproporre un vecchio articolo basato su una ricerca effettuata sulle api. E quando parliamo di istinto e di intelligenza stiamo molto attenti a non semplificare troppo la loro separazione.
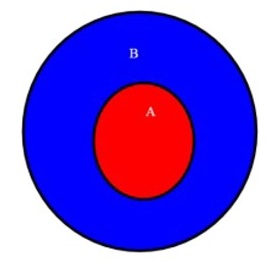
Tutti sappiamo come calcolare il numero di elementi di un insieme finito; basta contarli. E tutti più o meno sanno cosa sia un insieme infinito; ma gli infiniti sono tutti uguali? Lo scopo di questa serie di articoli sarà proprio questo, dimostrare che non sono tutti uguali.
Un semplicissimo e divertente quiz geometrico, veramente adatto a tutti, soprattutto ai bambini che iniziano lo studio della geometria. Genitori, proponetelo ai vostri figli e invitateli a ragionare. I “più bravi” del circolo aspettino almeno un paio di giorni, sperando di sentire finalmente qualche nuova voce!

I Papalcuriosoni sono un Team di Papallicoli specializzati nello smontare e rimontare giochi.
Appaiono spesso urlando a squarciagola : STOP AL PANICO!
Rispetto ai più semplici racconti dei Papallicoli i Papalcuriosoni affrontano giochi un pochino più complessi... ed i loro racconti necessitano di una maggiore attenzione... comunque sono sempre disponibili a provare a spiegare meglio ciò che potrebbe apparire poco comprensibile...
Non preoccupatevi..... i Papalcursioni compariranno solo ogni tanto...
Questo articolo va oltre la risposta diretta al quiz sull’urto papalliano (che abbiamo già dato). Cerca di descrivere il problema nella sua completezza e di dare risposte più ampie e generali. Come spesso in matematica, esistono vari sistemi per ottenere un certo risultato. In questo caso usiamo sia la geometria analitica sia gli sviluppi in serie, in modo che l’articolo diventi un riassunto di vari concetti, indipendentemente dal suo scopo vero e proprio. Come indicato vicino al titolo esso è stato scritto a sei mani (quelle di Paolo, di Umberto e le mie), dato che ognuno ha contribuito indipendentemente a formulare i diversi tipi di soluzione. Una collaborazione veramente vincente, che siamo sicuri si ripeterà in futuro. Il nostro circolo deve essere qualcosa di attivo e coinvolgente e non un’arida e unilaterale esposizione di concetti. Il mondo di Papalla e i Papallicoli ce lo dimostrano con estrema chiarezza.
In questo breve articolo rispondiamo soltanto alla domanda fatta a proposito del gioco papalliano, in cui due papalli corrono uno verso l’altro con la stessa velocità, mentre un elettrone, di dimensioni nulle, continua a far la spola (con velocità più alta) tra uno e l’altro. Il gioco ha, tuttavia, molti risvolti di tipo didattico e varie possibilità di ottenere risposte più articolate. Seguirà, perciò, quanto prima, un articolo un poco più complesso che sfrutterà le serie convergenti e un po’ di geometria analitica. Un articolo a tre mani, dato che un rilevante contributo alle sue varie sfaccettature è stato dato sia da Paolo che da Umberto. Un tipico lavoro d’equipe!
Così come avevamo creato una tabella per riassumere le derivate delle funzioni più comuni, così possiamo facilmente fare lo stesso con gli integrali corrispondenti. Se si vuole integrare una funzione f(x), che sappiamo immediatamente essere una derivata di una certa altra funzione F(x), possiamo identificare l’integrale con quest’ultima funzione. Ma, non sempre, le cose sono così semplici.
Le derivate comportano sicuramente dei problemi quando le funzioni sono piuttosto complesse. Tuttavia, con un po’ di attenzione e di pazienza, si riesce a portare a compimento l’esercizio. Insomma, le derivate spaventano, ma non poi tanto. Dovrebbe succedere lo stesso con gli integrali che sono l’operazione inversa. E, invece, come tutte le operazioni inverse, le difficoltà crescono di molto. Non è, quindi, assurdo giudicare gli integrali ben più ostici delle derivate. Capita a tutti, anche ai migliori matematici…


