Vi chiedo perdono per due motivi. Innanzitutto, perché il problema fisico (ma anche matematico) è di estrema semplicità. Inoltre, perché ho scritto un articolo di risposta assurdamente lungo per ciò che si chiedeva. Spero, però, che serva a fare un bel ripasso di derivate e limiti…
Volevo sospendere i quiz per un po'. Ma poi mi è venuto in mente questo semplicissimo esercizio, veramente alla portata di tutti dal punto di vista “fisico”. Tuttavia, esso può diventare un ottimo punto di partenza per un breve e utile ripasso di matematica, oltre che essere applicato ai pianeti, ai satelliti e alle stelle a noi più vicini… ma non solo. Ripeto, tutti, proprio tutti, si possono cimentare nel semplice calcolo e nelle sue conseguenze pratiche.

Ieri, 14 marzo, era il giorno dedicato al pigreco. Come piccola celebrazione vi propongo un simpatico metodo per calcolarlo con tante cifre decimali…
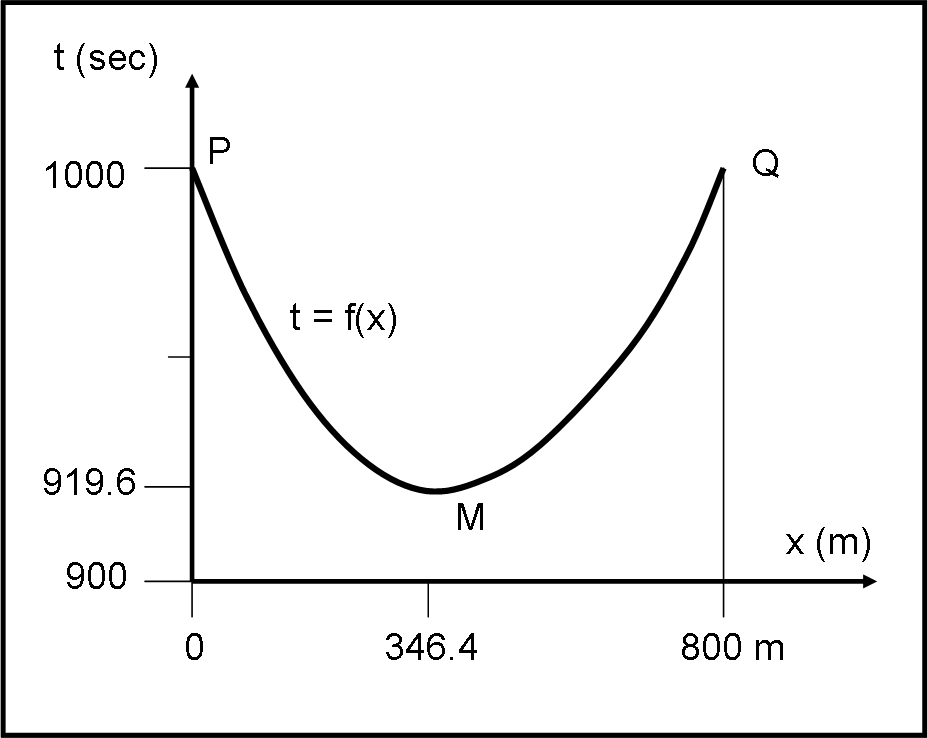
Approfittiamo della soluzione al quiz sul "naufrago" per fare un piccolo ripasso di derivate e di studio di funzione. Un caso veramente elementare... credetemi!
Siamo pronti a introdurre i flessi obliqui. Dopo quanto fatto finora, le regole che permettono di determinarli risultano ovvie, anche se bisogna porre attenzione al tipo di concavità che li precede e li segue: non sempre ciò che sale è ascendente! Iniziamo poi con lo studio dei polinomi più semplici…
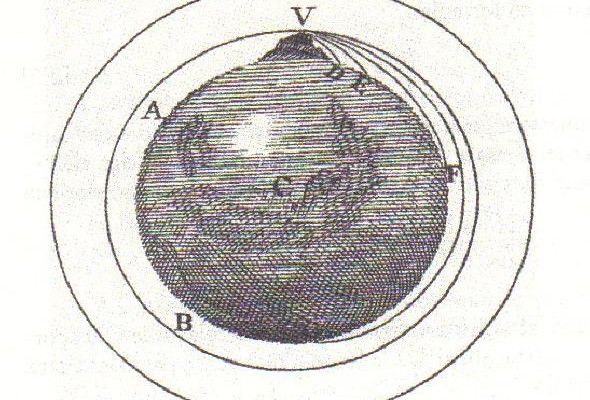
Se io rispondessi di no, qualcuno potrebbe dire che la Luna sta cadendo sulla Terra. Troppo spesso, infatti, si sente dire che la Luna non cade perché la forza centrifuga si oppone a quella centripeta. Purtroppo, c’è molta confusione a riguardo. Non ci resta che utilizzare la Luna per risolvere il problema. In questo articolo si ripassano velocemente i principi della dinamica e non solo. E’, quindi, estremamente sintetico. Ogni frase (anche se ripetuta, come mio solito) va compresa appieno perché definisce, spesso, concetti fondamentali per la comprensione della meccanica classica.
I satelliti di Giove hanno cominciato a giocare a nascondino tra di loro. Un fenomeno ricorrente che assume ancora un’importanza professionale. Vale la pena cercare di capire bene la configurazione geometrica che li rende possibili. Niente di difficile e completamente descrivibile con un foglio e una matita, senza bisogno di programmi prefabbricati che vengono presi a scatola chiusa. Sono sicuramente affascinanti, ma insegnano poco o niente. Continuo a lottare a favore della mente e contro la pappa pronta che vogliono imporci media e internet. Seguire questo lungo articolo è, inoltre, un fondamentale esercizio di geometria che non può che aiutare in contesti ben più generali. Spazio-tempo, multiversi, meccanica quantistica, relatività, ecc., ecc., sono argomenti affascinanti, ma senza le basi della geometria, della matematica e della fisica elementare, rimangono soprattutto belle "parole", ma sempre troppo lontane per essere veramente tangibili.
In questo file ho inserito tutti gli articoli riguardanti la matematica, dalla conoscenza delle zero e dell'infinito fino alle derivate e allo studio di funzioni. Il linguaggio è quello più semplice e adatto a tutti... Come dice il nostro Paolo: Non serve descriverne i tratti somatici, fissandoli nella propria memoria, la matematica ha bisogno di essere compresa per mostrare la sua semplicità, solo così il brutto carattere lascia il posto al sorriso.
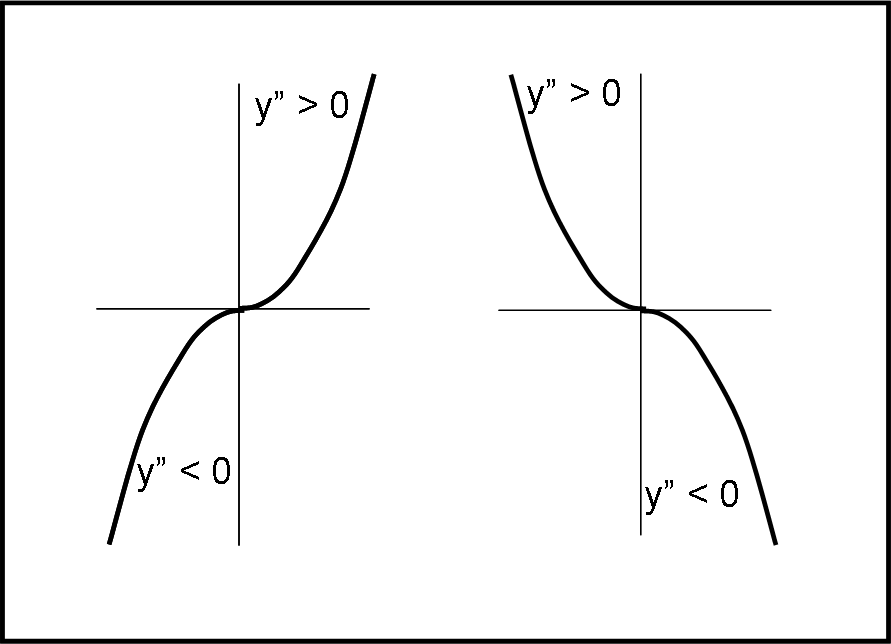
Dopo aver introdotto i massimi, i minimi e i flessi orizzontali in modo molto preliminare, è giunta l’ora di affrontarli più accuratamente attraverso le derivate successive di una funzione. Ci arriveremo lentamente in modo da comprenderne appieno il significato sia matematico che geometrico.

Gli spaghetti all’amatriciana sono buonissimi… i calcoli matriciali sono invece oltremodo complicati (e anche un po’ noiosi e- forse- indigesti). Questo breve articolo è un’appendice a quello del prodotto vettoriale, relativo al momento angolare (il terzo della serie). Come si dice normalmente… è destinato ai solutori più che abili. Tenete, comunque, conto che le matrici sono il linguaggio normale di molte parti della geometria analitica. Geometria 1 e 2 (che avevo seguito io) si basavano quasi solo su di loro… da far girare la testa…
E’ ora di tornare alla nostra matematica, dato che molti l’hanno seguita e vorrebbero proseguire. Abbiamo iniziato a studiare le funzioni e torniamo improvvisamente indietro a parlare di nuovo di retta, la funzione più semplice e la prima che abbiamo trattato… Sembrerebbe una cosa assurda.
In questo articolo ce n’è per tutti i gusti, come si vede dai vari gruppi di asterischi (difficoltà). La parte fondamentale, fino alla … “mano destra”, è abbastanza semplice e deve essere digerita da tutti coloro che vogliono andare avanti. Poi si passa a un piccolo esercizio e allo sviluppo attraverso le componenti (un piacere “estetico” non obbligatorio). Infine, chi non si accontenta ancora, può divertirsi con due vettori posti su un piano qualsiasi. In ogni modo, ho usato una trattazione piuttosto diversa dal solito che permette di spiare all’interno del mondo della dinamica rotatoria, dove il momento angolare ha un posto di primo piano.
Rimaniamo sempre tra i vettori, ma iniziamo a studiare il loro prodotto. Dato che i vettori sono grandezze veramente speciali non si accontentano di un solo prodotto, ma ne pretendono due. Cominciamo con quello “scalare”. Ci faremo aiutare dal grande Cyrano de Bergerac: “ed al fin della licenza io tocco!”
Cominciamo da lontano, ossia proprio dagli inizi. Per potere parlare di momento angolare bisogna prima conoscere molto bene cosa sono le grandezze fisiche e quali sono le operazioni che possono fare. In particolare, quelle relative ai vettori. Qualcuna la conosciamo già, ma le altre sono ancora abbastanza misteriose... Come faccio spesso, l'articolo si conclude con un piccolo esercizio che vi assicurerà di aver capito i concetti principali.
Cari amici, non sono molto contento dei risultati (lo dico perché siamo tra AMICI, ovviamente). Innanzitutto, perché solo pochissimi hanno risposto. Ma soprattutto non mi è piaciuto il modo come hanno risposto. Perché? Quasi tutti non hanno seguito il semplice procedimento che avevo illustrato nel capitolo 24, ma hanno liberamente utilizzato concetti e procedimenti che ancora non avevo spiegato. Tutto ciò può dimostrare che loro sono bravi e preparati, ma ha creato molta confusione nei meno preparati. Probabilmente aiutandoli a lasciar perdere un argomento che si stava complicando in modo non gestibile attraverso le lezioni già pubblicate. Insomma, siamo caduti nel solito errore che fa odiare la matematica: la perdita di un ordine semplice, chiaro e umile. Il succo delle 24 lezioni non è, invece, questo e nemmeno quello di fare classifiche di bravura, ma solo quello di tentare di fare amare una materia fondamentale per capire l’Universo.
Attraverso il capitolo 24 siamo ormai in grado di calcolare i punti particolari di funzioni abbastanza semplici. Scopriremo che esistono anche altri punti peculiari e altri metodi di calcolo, ma per adesso accontentiamoci di quanto descritto finora. Forza, le vacanze sono finite e si torna al lavoro! Un piccolo test prima di andare avanti. Se non riuscite… ditelo senza vergogna (magari in privato), in modo che possa intervenire subito. Sarebbe assurdo continuare se sono sorti dei problemi già adesso.

