Cominciamo a calcolare alcune derivate di funzioni particolari, rappresentate dai semplici monomi. Una rapida analisi dei risultati ci insegna che esiste una facile regola generale che evita il noioso passaggio attraverso il rapporto incrementale. Segue un’appendice per i più … volenterosi.
Se io rispondessi di no, qualcuno potrebbe dire che la Luna sta cadendo sulla Terra. Troppo spesso, infatti, si sente dire che la Luna non cade perché la forza centrifuga si oppone a quella centripeta. Purtroppo, c’è molta confusione a riguardo. Non ci resta che utilizzare la Luna per risolvere il problema. In questo articolo si ripassano velocemente i principi della dinamica e non solo. E’, quindi, estremamente sintetico. Ogni frase (anche se ripetuta, come mio solito) va compresa appieno perché definisce, spesso, concetti fondamentali per la comprensione della meccanica classica.
In questa parte, veramente fondamentale, calcoliamo la prima derivata di una funzione che non sia una retta e ne diamo il significato geometrico. Lo scenario si amplia sempre di più.
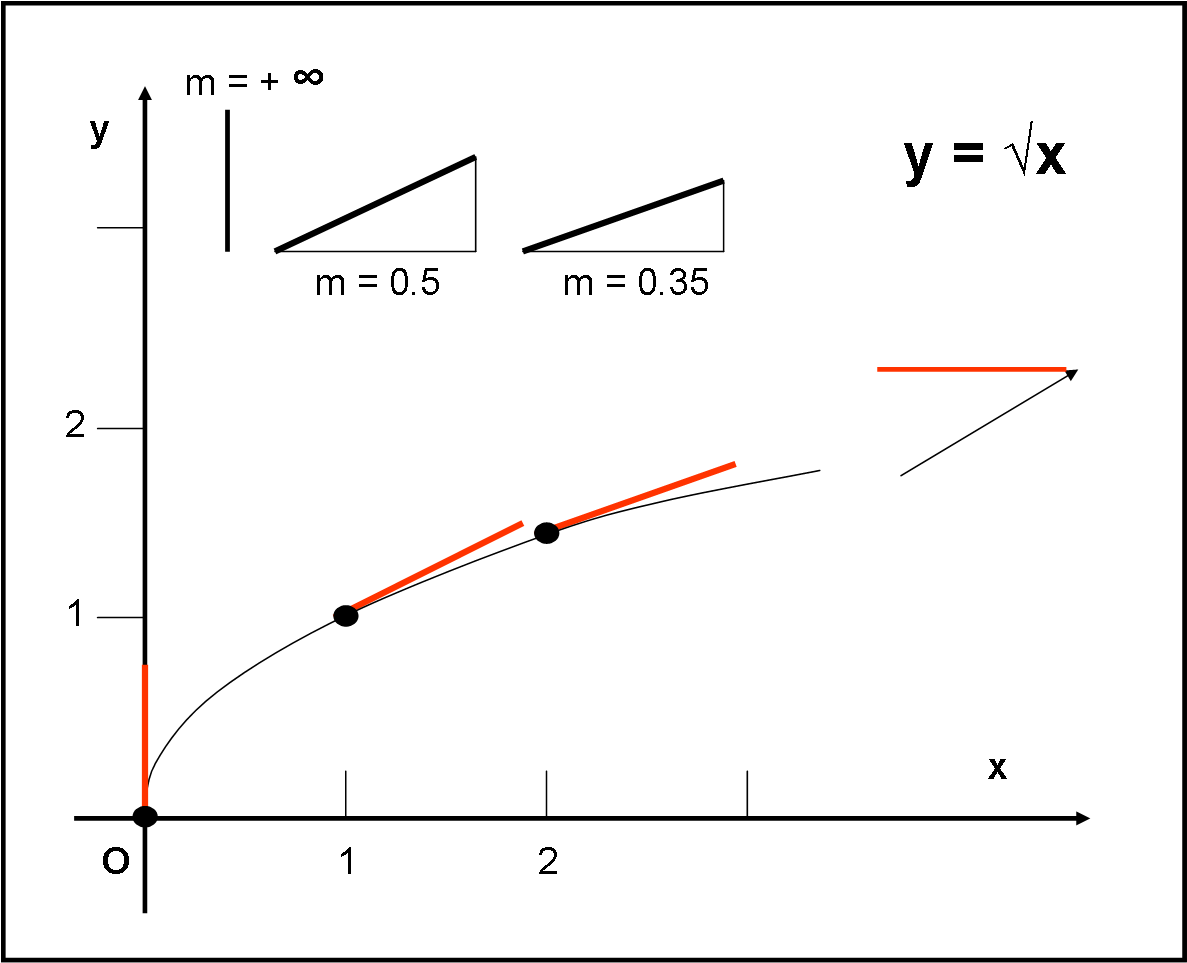
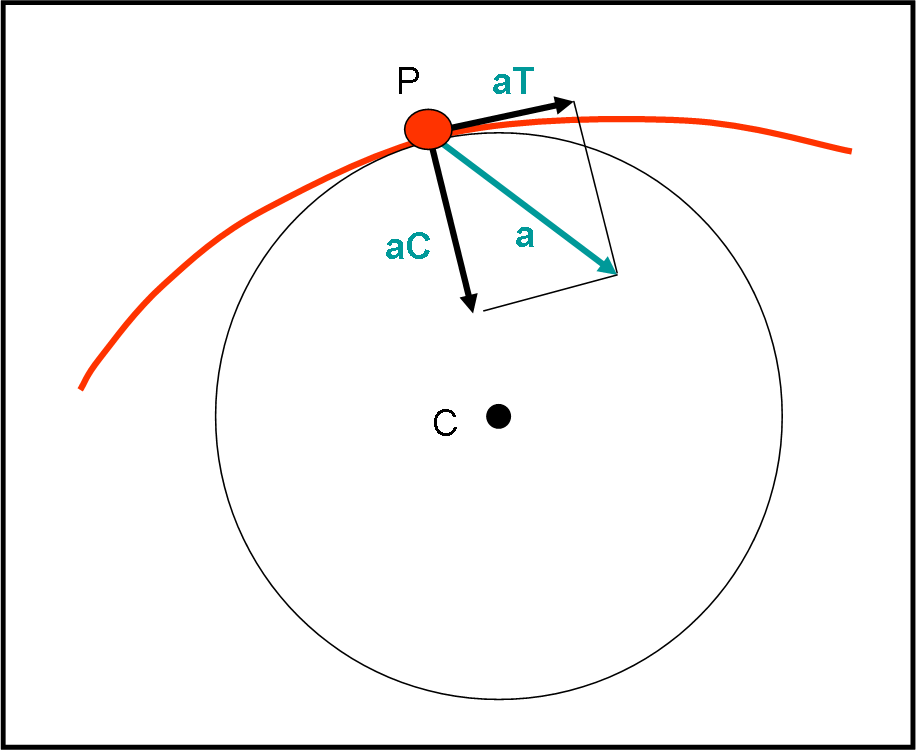
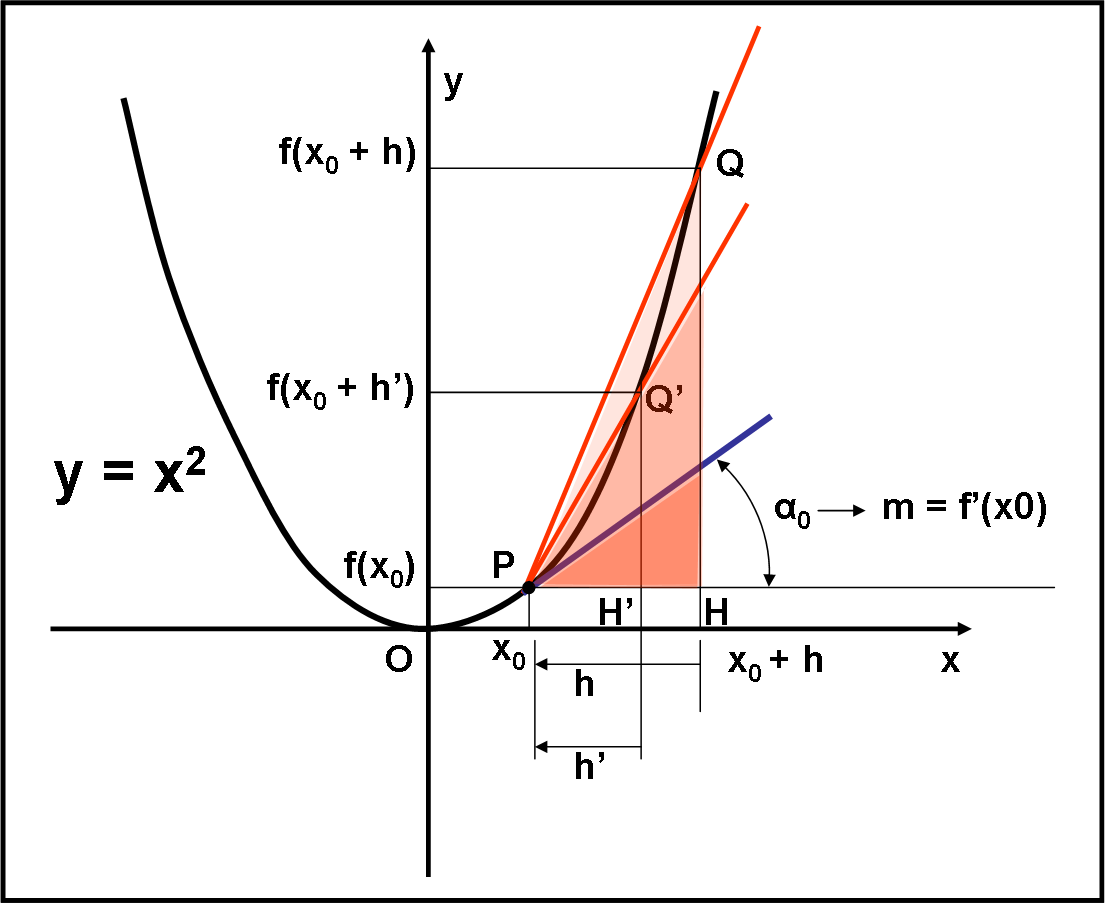
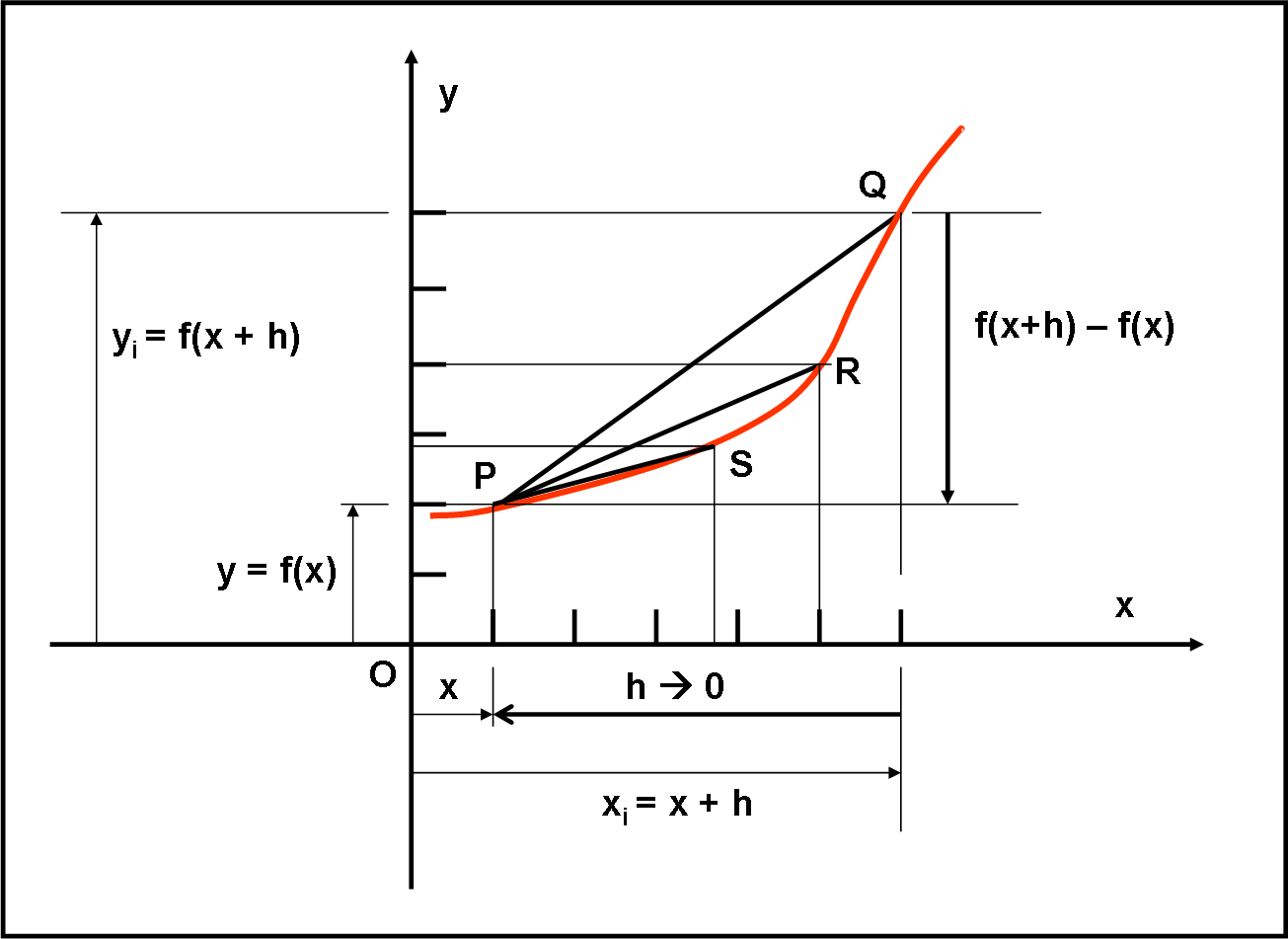
Siamo arrivati a un punto fondamentale: l’introduzione della derivata di una funzione. Iniziamo col descriverla in modo estremamente semplificato, quanto basta per afferrare il concetto base. Poi, compresa la sua ragione di esistere, vedremo di utilizzare la matematica che già conosciamo per utilizzarla al meglio. Un passo alla volta. Ho usato una strada lunga e ho girato molto attorno al problema. L’ho fatto sperando di semplificare. Tuttavia, questo è forse l’articolo più importante per entrare nel mondo della matematica “superiore” e, quindi, comunicatemi ogni pur piccolo dubbio abbiate e cercherò, se necessario, anche di cambiare la trattazione se per qualcuno risulta ancora difficile. Scrivo queste “lezioni” per voi e quindi aiutatemi a migliorarle… mi raccomando! Come al solito, ho reso l’articolo simile a un’avventura… un’avventura “matematica”, ovviamente!
Abbiamo già parlato delle più semplici funzioni trigonometriche. Sia perché ci sono servite per definire il coefficiente angolare di una retta, sia perché attraverso di loro si può passare da un sistema di coordinate cartesiane a uno di coordinate polari (e viceversa). L’uso delle funzioni trigonometriche permette, in genere, di calcolare facilmente le componenti di un segmento qualsiasi rispetto ai due assi cartesiani. E mille cose ancora… Tuttavia, restano comunque delle funzioni ed è giusto studiarle come abbiamo fatto per le coniche, le rette, il logaritmo e cose del genere.
L’uso della funzione esponenziale, in particolare di quella che si basa sul numero e, permette di descrivere la celebre spirale logaritmica. Essa rappresenta un passo in più rispetto a quella di Archimede, anche se è altrettanto semplice ed è la curva più utilizzata nel Cosmo, a tutti i livelli di grandezza. Oltretutto, ha anche influenzato le proporzioni armoniose dei monumenti, delle statue e delle pitture, a partire dai capolavori greci (rettangolo aureo). Ovviamente, ha a che fare con i numeri di Fibonacci.
Come già detto, prima di arrivare alla spirale logaritmica, legata strettamente al numero e, soffermiamoci un momento su una spirale più “semplice” che ha, però, permesso ad Archimede di risolvere problemi matematici che sembravano insuperabili. Ci serve anche per fare un po’ di sano esercizio “matematico”.
Venerdì prossimo ricorre una festa molto speciale. Solo un cenno per ricordare un numero veramente astronomico!
Passiamo alla definizione di un numero molto particolare e di una funzione che non fa altro che elevarlo a un certo esponente variabile. Concettualmente niente di difficile. Anzi, sembrerebbe una scelta un po’ strana se non sapessimo quanto la Natura ama questo numero così bizzarro e fondamentale.
Se la volta scorsa vi avevo “martellato” duro, questa volta vi vengo incontro. Poche righe per definire le coniche in un modo matematico ben più ampio e generale. Tuttavia, non andremo nei dettagli e ci limiteremo al concetto base. Chi ha, però, voglia di divertirsi ha tutti i mezzi a sua disposizione.
Lo ammetto: questa parte è abbastanza lunga e pesante. Inoltre, necessita di grande attenzione e riflessione. Cercate di seguirla con calma senza farvi prendere dalla noia o dall’ansia di arrivare alla fine. L’iperbole è troppo importante in fisica per “snobbarla”. Se riuscite a seguire tutti i passaggi, siete già a buon punto per considerarvi matematici “abbastanza” esperti.
Abbiamo descritto la conica che rappresenta una curva chiusa e che ha come caso particolare la circonferenza. Manovrando il piano-coltello si arriva a un punto critico: quello in cui la curva si apre e diventa una parabola. Un caso limite anch’esso, ma altrettanto importante.
Dopo aver fatto il lavoro dei “salumai”, affettando un salame conico, vediamo di analizzare un po’ meglio le “fette” che abbiamo ottenuto. Introduciamo anche la matematica e troviamo nuovamente le nostre care funzioni. Cominciamo con l’ellisse e la sua figlia prediletta, la circonferenza.
Volevo solo “sfiorare” le coniche, considerandole come altre funzioni che impareremo a studiare nei dettagli. Tuttavia, la loro enorme importanza mi ha bloccato e convinto che meritano qualcosa di più. L’articolo è diventato chilometrico, per cui lo divido in cinque parti. Non solo matematica, ma anche tanta geometria. Cominciamo… affettando un cono con un coltello molto affilato.
Iniziamo con una funzione che dovrebbe essere ben nota a tutti gli appassionati di astronomia, dato che si lega strettamente alle magnitudini stellari. La sua importanza è, però, decisamente superiore e il suo utilizzo vastissimo in tutti i campi della Scienza. Introdurremo quello in base 10, ma in seguito conosceremo anche quello che ha per base uno dei “magici” numeri della matematica.
Rilassatevi. Questo articolo è veramente corto e non è altro che la descrizione di una mia riflessione che ha portato ad una scelta. Non so se è quella migliore, sarete poi voi a dirmelo. Come già detto, potremo sempre invertire l’ordine degli addendi: il risultato non cambierebbe.