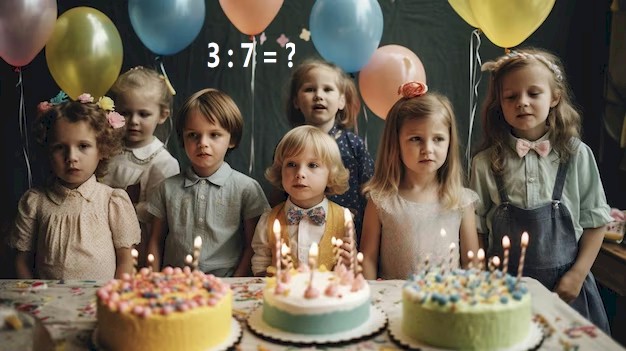Mentre su Krull ciascuno ha la propria casa, sulla Terra, dove ci sono nove miliardi di abitanti, capita che una casa appartenga contemporaneamente a più persone. Ciascuno ne possiede una parte, e per far capire a tutti quanta se ne possiede si sono inventati i millesimi, una cosa micidiale.