Una applicazione del'assioma della scelta porta ad una situazione paradossale; non tutti gli insiemi possono essere misurati. Lo ha dimostrato Vitali .
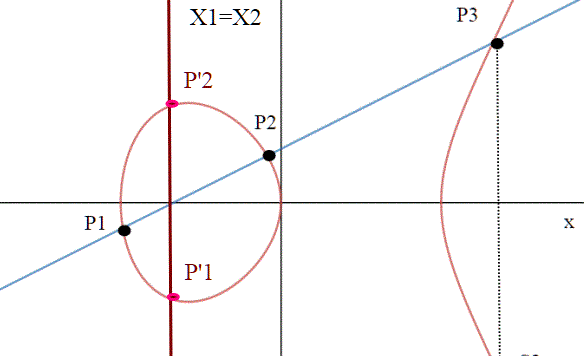
Un riassunto su tutto quello che abbiamo visto sulle curve ellittiche,quiz compresi, che ci porta a concludere che esse costituiscono un gruppo con una particolare operazione interna. Questo fatto è fondamentale per l'impiego delle curve ellittiche in crittografia.
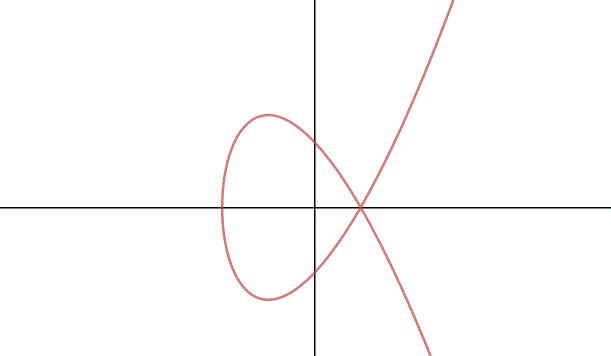
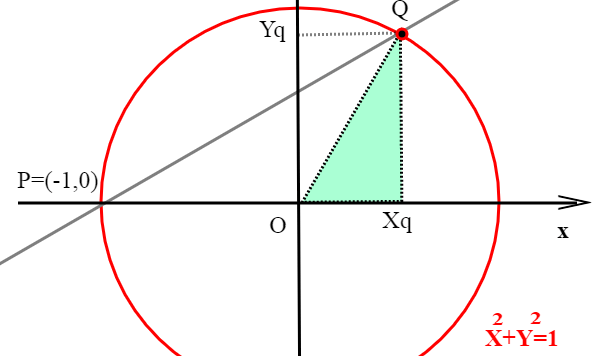
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Riprendiamo il discorso sulle curve ellittiche; nell' articolo precedente (qui), abbiamo trovato il punto all'infinito di una curva ellittica di equazione generica: ; esso coincide con il punto all'infinito dell'asse delle y; questo ci fa capire che la curva all'infinito è tangente all'asse delle y. […]
Se vogliamo parlare in modo totalmente corretto di equazioni ellittiche e di gruppi ellittici dobbiamo farlo all'interno del piano proiettivo. E' necessario introdurre il concetto di punto improprio o punto all'infinito, con una trattazione non strettamente formale, ma più che altro intuitiva.
In questo articolo finiamo la nostra (breve) trattazione sui numeri complessi; lo scopo è quello di fornire i strumenti minimi i calcolo che ci permettano poi di affrontare argomenti più complicati. Parleremo delle elaborazioni di due grandi personaggi della matematica: Newton e Eulero.
Per gli sviluppi delle nostre matematiche pure è necessario conoscere i numeri complessi, che forse non tutti hanno avuto la fortuna di studiare.I numeri complessi sono forse i numeri più affascinanti della matematica. Essi trovano applicazione in varie branchie della fisica (basti citare l'elettrotecnica e la meccanica quantistica). I primi scritti sicuri sui complessi sono attribuiti a Carl Friedrich Gauss (1777, 1855) la mente più privilegiata della matematica moderna.
Ho voluto fare un esempio di applicazione dei gruppi ciclici e dei campi su Zp (interi modulo p) per far capire che anche questa matematica un po' strana ha una applicazione fondamentale nella gestione della sicurezza delle informazioni. Senza saperlo, ogni volta che usiamo la carta di credito, usiamo anche i gruppi algebrici.
Per analizzare correttamente le equazioni algebriche sotto nuovi punti di vista (tipo quelle ellittiche usate da Wiles per la dimostrazione della congettura di Fermat) bisogna avere a disposizione una nuova struttura algebrica: il Campo. Nell'immagine Euclide; i suoi algoritmi sono ancora attuali perfino nelle moderne congetture matematiche.
Qual'è la cardinalità del piano? A occhio e croce ben di più di quella della retta, che ha cardinalità c, pari dunque a quella dei numeri reali. Invece avremo una gran bella sorpresa: la cardinalità del piano è uguale a quella della retta. Questo fatto è fortemente controintuitivo. Lo stesso Cantor , in una lettera a Dedekind ,dove ne riporta la dimostrazione, scrive: "Lo vedo, ma non lo credo".
Come tutti avranno capito , la parte iniziale del quiz che trovate QUI non ha soluzione, ovvero per n>2 non è possibile trovare degli interi a,b,c tali che: per n>2 e che altro non costituisce che l'ultimo teorema di Fermat, Useremo la sigla UTF per indicare tale teorema; in realtà sarebbe più corretto chiamarlo teorema di Wiles, […]
Nell'articolo precedente abbiamo parlato di generatori di gruppi e di gruppi liberi. Vogliamo ora provare l'esistenza di questi gruppi, senza ricorrere ad un esempio "reale", ma costruendo un gruppo libero partendo da un insieme qualsiasi. Notiamo così ancora una volta che la matematica non è solo una scienza logico-deduttiva, ma soprattutto creativa,costruttiva.
Questo articolo è un po' più difficile di quelli trattati finora, richiede una buona capacità di astrazione. Vedremo come generare un gruppo partendo da un insieme qualsiasi. Qualcuno si chiederà a cosa può servire una cosa del genere.. vi anticipo solo che è fondamentale per comprendere uno dei più importanti paradossi della matematica moderna, quello di Banach-Tarski.
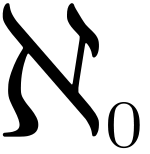
In questo articolo ci proponiamo di dare la definizione di numero cardinale usando il concetto di classe di equivalenza visto nell'articolo precedente. Ne approfittiamo anche per introdurre la funzione inversa e la funzione composta di una funzione, a complemento di quanto già visto nell'articolo su corrispondenze e funzioni.
Le relazioni e le classi di equivalenza aprono un altro capitolo estremamente importante della teoria degli insiemi. Tramite le classi di equivalenza è stato possibile formalizzare correttamente le definizioni di numero intero, razionale ed altro ancora. In poche parole costruire una base solida della matematica.
La congettura che ogni insieme può essere ben ordinato presupposta da Cantor , fu dimostrata da Zermelo con il teorema sul buon ordinamento. Tale teorema ci porta immediatamente ad un'importante conseguenza; gli ordini d'infinito di due insiemi qualsiasi sono sempre confrontabili.
Il teorema di Zermelo afferma che ogni insieme può essere bene ordinato. Questo va dimostrato con il lemma di Zorn, che deriva dall'assioma della scelta. Georg Cantor considerava che questo enunciato fosse un "fondamentale principio del pensiero". Il lemma di Zorn (oppure l'equivalente assioma della scelta) ha anche conseguenze che possono apparire paradossali, come ad esempio il cosiddetto paradosso di Banach-Tarski.