Category Archives: "Teoria degli insiemi"

Il teorema di Zermelo afferma che ogni insieme può essere bene ordinato. Questo va dimostrato con il lemma di Zorn, che deriva dall'assioma della scelta. Georg Cantor considerava che questo enunciato fosse un "fondamentale principio del pensiero". Il lemma di Zorn (oppure l'equivalente assioma della scelta) ha anche conseguenze che possono apparire paradossali, come ad esempio il cosiddetto paradosso di Banach-Tarski.

Questo articolo sarà completamente dedicato alla dimostrazione di un importante teorema sugli isomorfismi, essenziale per la comprensione del lemma di Zorn: la Tricotomia degli insiemi bene ordinati.

Questo è il primo di una miniserie di (tre) articoli dedicati unicamente al lemma di Zorn. Per poter enunciare il lemma di Zorn, è necessario conoscere certe definizioni e certi risultati sugli insiemi ben ordinati. Sfrutteremo poi il concetto di catena per esplorare gli insiemi parzialmente ordinati.

Nel 1904 Zermelo pubblicò una prima versione della teoria assiomatica degli insiemi, che comprendeva anche l'assioma della scelta. Tale assioma ha importanti conseguenze in molti  rami della matematica contemporanea (basti pensare all'analisi funzionale che è alla base dell'apparato teorico della meccanica quantistica)  e ciò ha senz'altro contribuito a far sì che sia oggi diffusamente accettato. Per quanto ci riguarda , per noi è necessario per dimostrare la confrontabilità fra numeri cardinali.

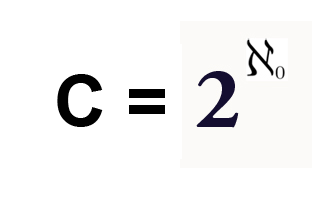
Ci stupiamo ancora una volta di come l'assioma di continuità e una sua importante conseguenza (l'assioma di Archimede) , svolgano una parte essenziale nelle dimostrazioni riguardanti la cardinalità di R.

L'insieme di Cantor, anche detto polvere di Cantor, ci servirà per provare che la cardinalità dell'insieme delle parti è minore o uguale a quella del continuo (R).L'insieme è anche un primo approccio al mondo fantastico dei frattali; nella figura una versione tridimensionale dell'insieme di Cantor.

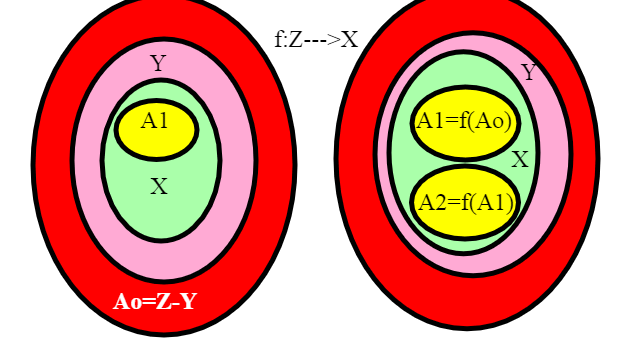
Il teorema di Bernstein risulta necessario per affinare il confronto fra i numeri Cardinali, ed è uno dei teoremi più importanti della teoria degli insiemi.La dimostrazione è complessa ma non estremamente difficile, Vedremo come il concetto di ricorsione, già applicato in altri contesti, occupi una parte dominante nella dimostrazione.

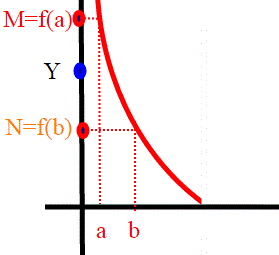
In questo articolo dimostreremo che R non è un insieme numerabile. La dimostrazione sarà quasi immediata servendoci dei risultati dell'articolo precedente, sulle conseguenze della continuità di R. Per giustificare il fatto che ogni intervallo di R è equipotente ad un suo intervallo, ho dovuto rifarmi a importanti teoremi di analisi matematica, di cui però ho dato la dimostrazione in appendice.

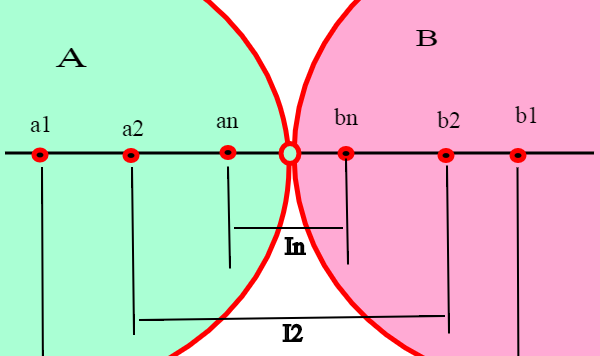
Siamo quasi pronti per dimostrare la non numerabilità dell'insieme dei numeri reali. Purtroppo senza alcune proprietà della continuità di R, non è possibile darne un dimostrazione convincente. Di solito si fa in quattro righe sfruttando la notazione decimale dei numeri reali e il secondo metodo diagonale di Cantor; a parte il fatto che la notazione decimale comporta alcuni problemi di non univocità , essa non è una delle cose più semplici da capire a fondo e inoltre deriva sempre dalle costruzioni di Dedekind e quindi dall'assioma di continuità

Cercare di analizzare la cardinalità di R senza prima parlare della continuità che lo caratterizza è assurdo; le dimostrazioni infatti si appoggiano appunto sulla continuità dei numeri reali. E' per questo che l'ordine di infinito di R è diverso (come vedremo) da quello degli insiemi numerabili: a causa della continuità. Lo stesso Cantor per primo, fece una costruzione dei numeri reali per raggiungere lo scopo, noi considereremo però la costruzione di Dedekind.

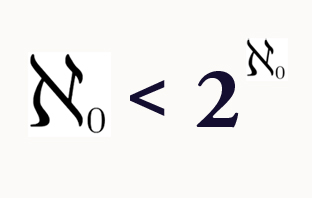
Nell'articolo precedente, abbiamo visto che anche Q è numerabile. Esistono insiemi non numerabili? Si, e lo dimostreremo in modo generale, arrivando ad un risultato di notevole importanza: non esiste un insieme di cardinalità maggiore di ogni altro insieme.

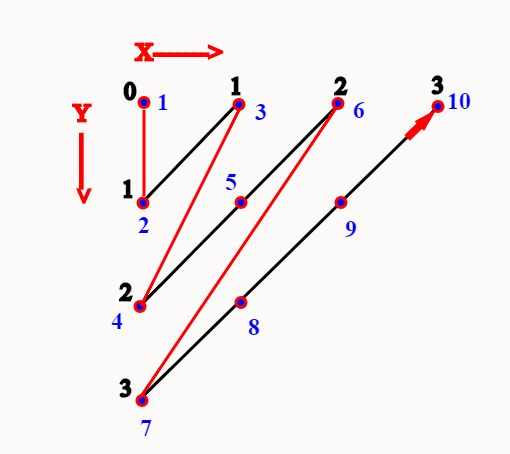
Adesso che sappiamo che N x N è numerabile, e che ogni sottoinsieme infinito di un insieme numerabile è numerabile, possiamo dimostrare che,malgrado l'apparenza, anche l'insieme Q è numerabile.

Abbiamo visto che un insieme numerabile contiene dei sottoinsiemi propri, che sono anch'essi numerabili. L'esempio era stato quello dei numeri pari e dei numeri dispari, che possono essere messi in corrispondenza biunivoca con l'intero insieme N. Consideriamo adesso un qualsiasi sottoinsieme proprio infinito X di N. Quale sarà sarà la sua cardinalità? Di sicuro X non potrà essere più numeroso di N, in quanto ha meno elementi (l'inclusione è propria). Vogliamo dimostrare che la sua cardinalità è ancora Aleph(0), che è la cardinalità di N.

Il principio di induzione matematica consente di risolvere in modo molto semplice delle dimostrazioni nell'ambito dell'insieme dei numeri naturali. Mi è sembrato perciò necessario introdurlo in questi articoli, in quanto ci servirà per dimostrare delle proprietà importanti sugli infiniti numerabili.

Dopo alcuni prerequisiti essenziali finalmente stiamo cominciando ad intraprendere il nostro viaggio nel Paradiso di Cantor, quello degli insiemi infiniti: gli insiemi numerabili.