Un quiz che ha sicuramente molte possibili soluzioni. Non fatevi, però, ingannare dalle apparenze...
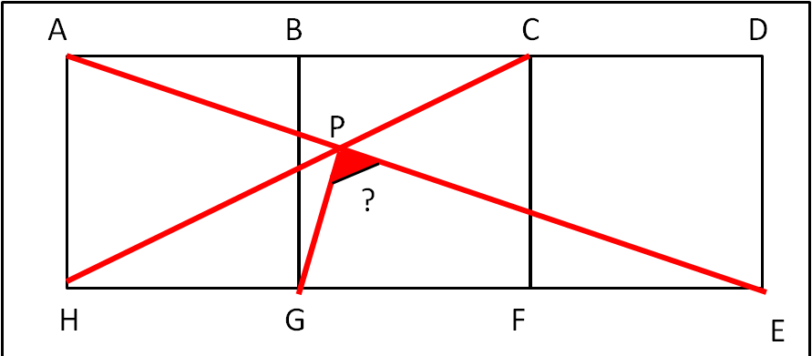

Un quiz che ha sicuramente molte possibili soluzioni. Non fatevi, però, ingannare dalle apparenze...
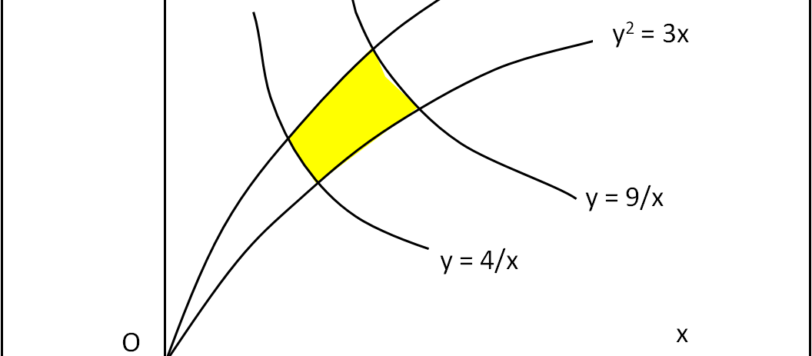
Un esempio un po' più complicato che ci permette di utilizzare (volendo) una proprietà dello Jacobiano.
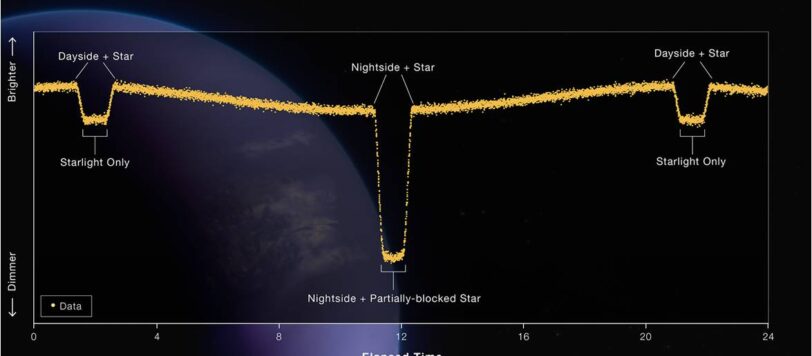
Le straordinarie capacità di Webb sono riuscite a descrivere la temperatura dell'atmosfera e la sua composizione di un pianeta gioviano caldo a 280 anni luce da noi. Insomma, è più facile fare le previsioni su pianeti extrasolari che sul nostro, dove la meteorologia è legata a interessi che di scientifico hanno ben poco.
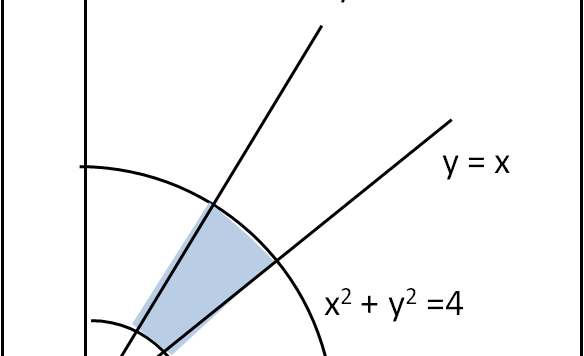
Due esempi di calcolo dell'integrale doppio relativo a una funzione φ(x,y), effettuato con un idoneo cambiamento di coordinate. Una specie di ripasso delle puntate precedenti...
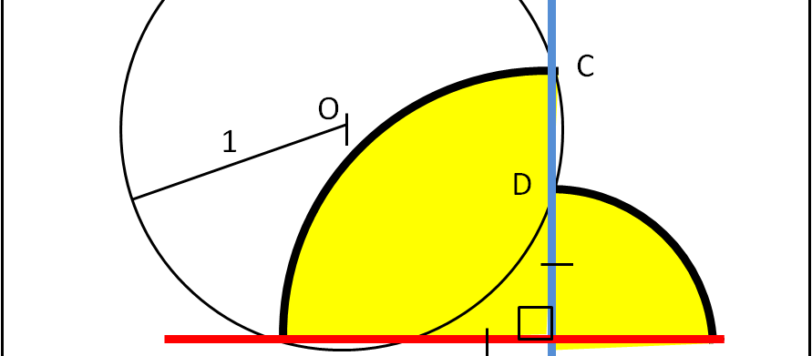
Un quiz che abbisogna di ragionamento, ma che può essere risolto praticamente con un paio di passaggi.

Introduciamo il determinante jacobiano, una specie di fattore di scala che ci permette di passare da un'area delimitata da funzioni più o meno complicate ad un'area dal contorno decisamente più semplice.
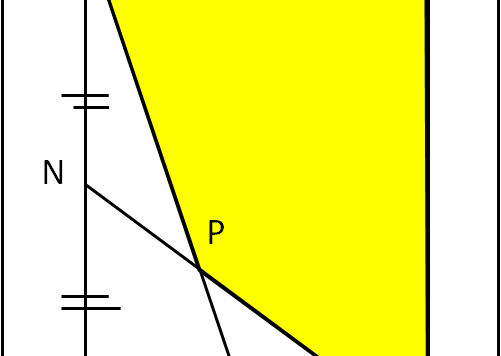
Insisto con i quiz geometrici dato che geometria (anche la più semplice) è fondamentale per gli studi sia matematici che fisici.

Affrontiamo passo dopo passo la possibilità di cambiare il dominio di integrazione di un integrale doppio per rendere il tutto più rapido e "facile".
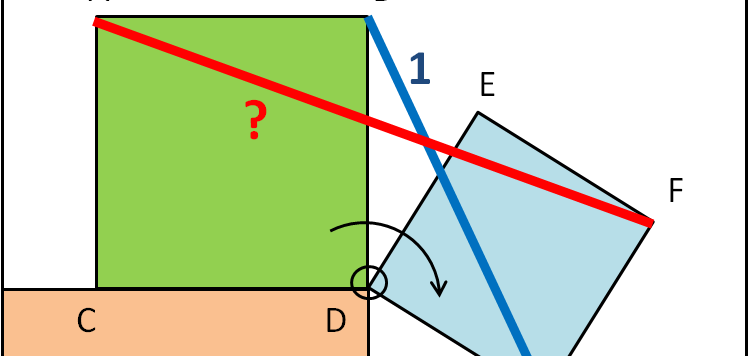
Un puro e (teoricamente) semplicissimo esercizio di geometria, applicato a un problema di equilibrio: la geometria è sempre indispensabile!
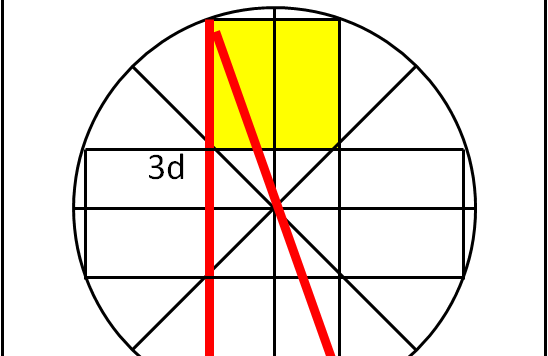
Questo quiz è veramente banale ed è rivolto praticamente solo ad Andy. Sarebbe bello se qualcuno lo battesse sul tempo e/o - almeno- lo imitasse. La difficoltà è veramente irrisoria.
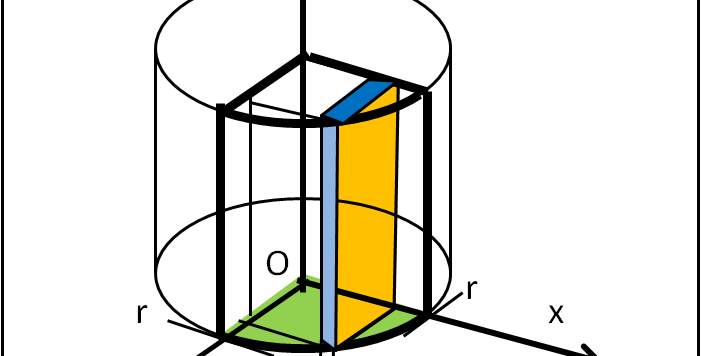
Come chiesto da Alberto, iniziamo col calcolare il volume del cilindro seguendo passo dopo passo quanto riportato nell'articolo sugli integrali doppi. Ci accorgeremo che si possono usare metodi alternativi molto più veloci.
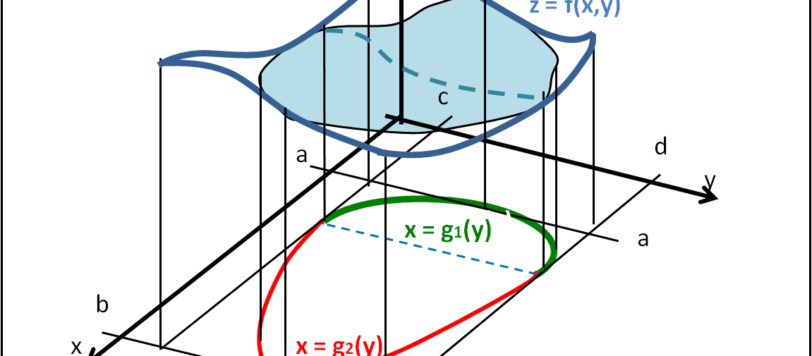
Meglio tardi che mai. Introduciamo gli integrali doppi, ossia il metodo per calcolare i volumi.