Nella vita niente è mai del tutto inutile. Si può sempre imparare qualcosa.

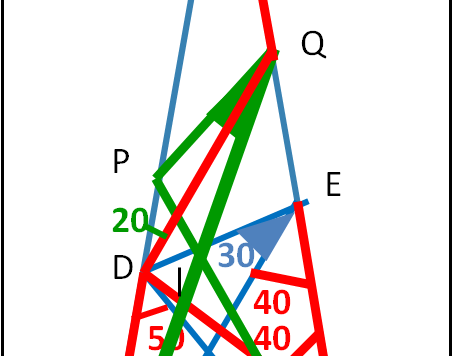
Le soluzioni di Maurizio e Andy sono ovviamente giuste (magari completatele...), ma fanno uso dei criteri di similitudine, concetto che non avevo previsto nel testo del quiz. In questo articolo trovate, invece, la soluzione di un quiz estremamente simile, sempre relativo al triangolo 80-80-20, ottenuta senza usare similitudini. Questa soluzione facilmente aiuta ad ottenere anche la soluzione al quiz originario. Volete provare ad aiutarmi?

Guardando tra vecchi archivi ho recuperato qualche racconto che, allora, avevo giudicato "minore". Beh... forse, in alcuni casi, mi sbagliavo. Ve li voglio riproporre sperando in una benevola risposta...

Il più difficile dei problemi facili. Provate con i vostri figli e/o nipoti e potrete vedere quanto la tecnologia della "pappa pronta" può aver influito sulla loro preparazione scolastica.

Avendo già introdotto la cinematica rotazione, lasciatemi proporre un semplice problema legato alle lancette dell'orologio...
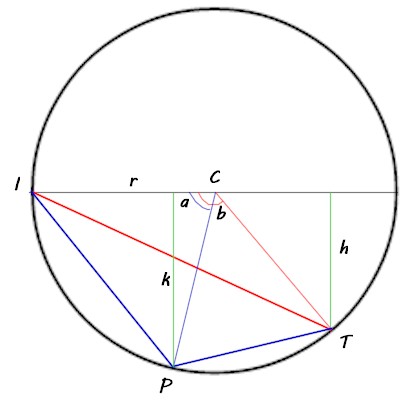
In questo breve articolo viene proposta una soluzione analitica alternativa a quella cinematica del quiz sulla corsa sugli slittini.
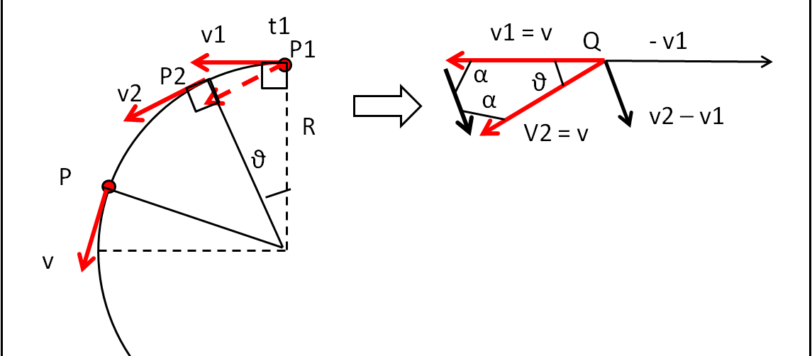
Descriviamo un altro moto veramente fondamentale in cinematica, quello circolare uniforme e suo fratello, il moto armonico.
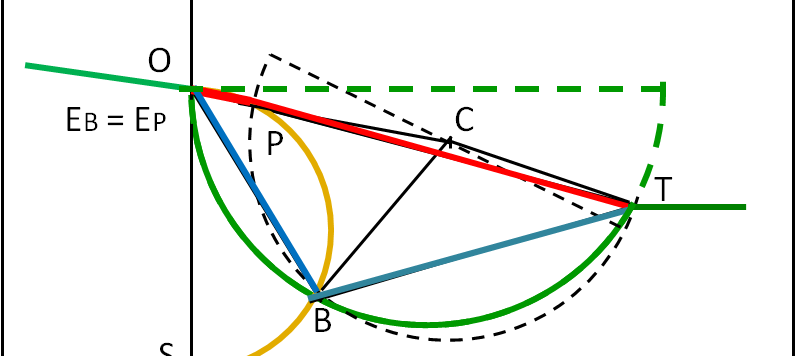
Pensavo fosse più semplice di quanto dimostratosi. I miei ringraziamenti, comunque, vanno a Michele e Mau per averci provato! Il quiz diventa un utile ripasso del piano inclinato...

Una eccezionale unione tra due stelle di neutroni ha permesso al telescopio Webb di individuare la presenza di elementi pesanti, come il tellurio, lo iodio e il torio.
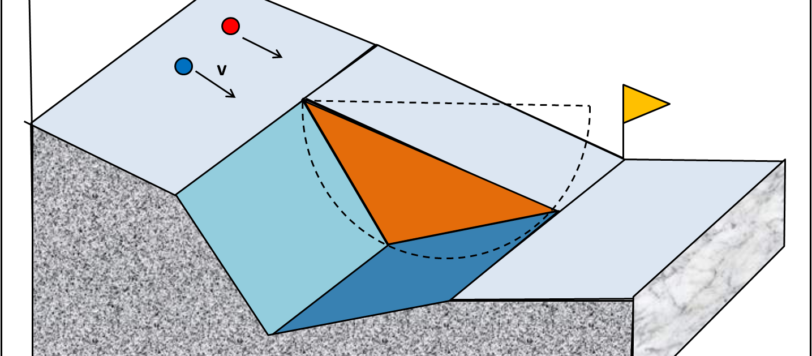
Dopo aver svolto insieme un certo numero di esercizi, è ora di mettervi alla prova sulla cinematica. Un'occasione per conoscere i due personaggi che hanno dato luogo al mio libro divulgativo di meccanica.

La Luna non vuole essere da meno e ci manda un'astronave per tenerci d'occhio... Alieni? No, meccanica celeste!
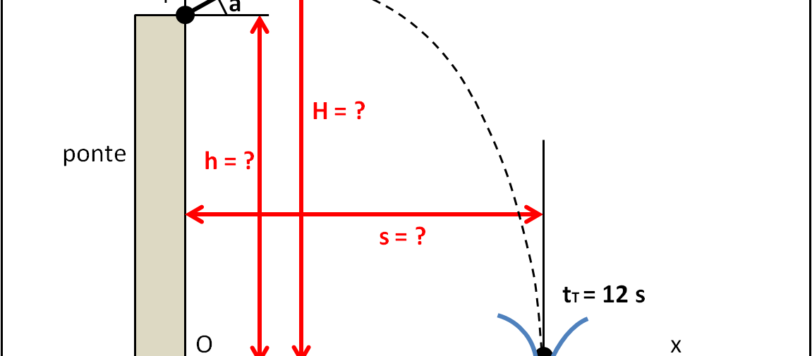
Ancora un paio di esercizi svolti assieme sulla cinematica bidimensionale e poi passeremo a un paio di quiz per mettere alla prova i meno esperti. Fatto questo ci occuperemo del moto circolare uniforme.
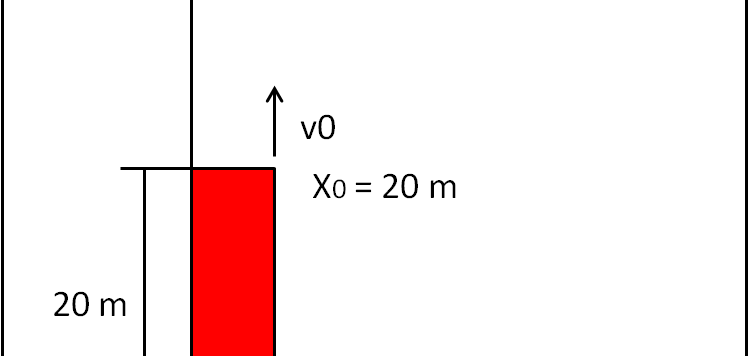
Un paio di esercizi di moto uniformemente accelerato, con l'applicazione della formula di Torricelli.