Completiamo la serie di articoli sui limiti notevoli e sulle derivate fondamentali. Spero, come sempre, che Albertone evidenzi gli errori di scrittura, quasi sicuri in questo periodo....


Completiamo la serie di articoli sui limiti notevoli e sulle derivate fondamentali. Spero, come sempre, che Albertone evidenzi gli errori di scrittura, quasi sicuri in questo periodo....
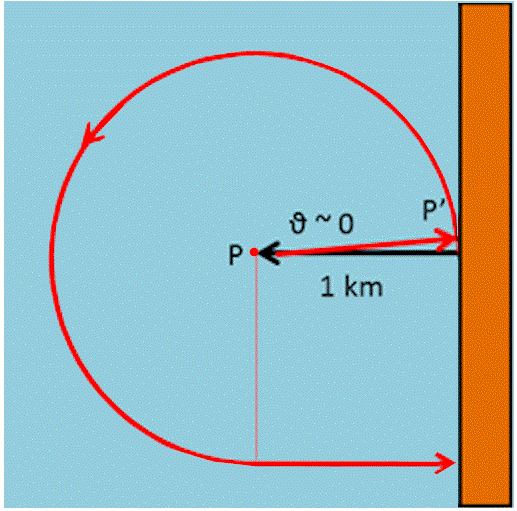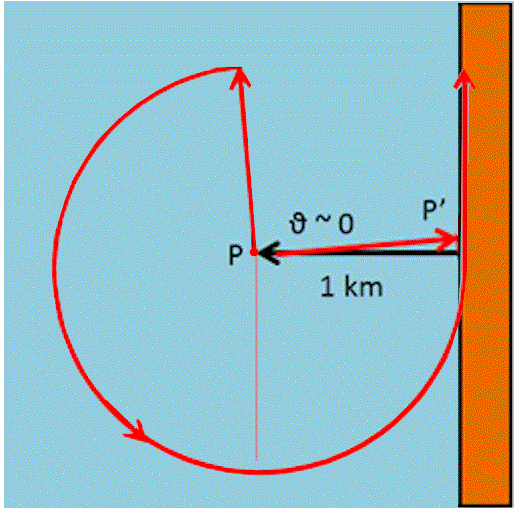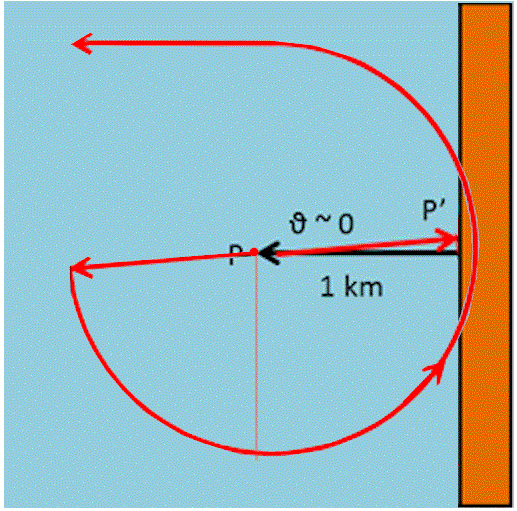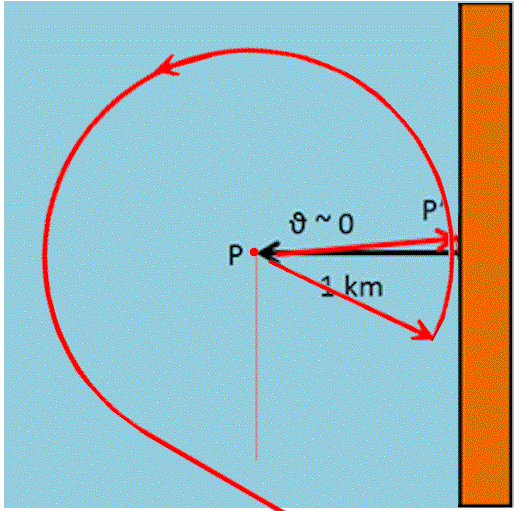
Siete in mare, lontano dalla costa e improvvisamente cala una nebbia fittissima... Un po' di semplice trigonometria vi può salvare la vita!
Andy e Maurizio si sono scatenati arrivando rapidamente alla soluzione e andando ben oltre. Io riposto, modestamente, solo l'indispensabile per entrare nella stanza...

Talvolta è sufficiente un nuovo punto di vista, un’inedita prospettiva o un angolo di luce differente e un oggetto dalle sembianze familiari ci offre un inconsueto aspetto di sé, qualcosa che rinnova l’interesse ai nostri occhi e, subito appresso, stimola la nostra mente famelica.

In un precedente articolo abbiamo visto le conseguenze di una improvvisa frenata della Terra nella sua rotazione orbitale e, in uno successivo, abbiamo anche visto cosa accadrebbe se la Terra smettesse “semplicemente” di girare su sé stessa. Oggi, grazie alla testimonianza di chi ha vissuto l'evento descritto in quel secondo articolo, possiamo fornire ai lettori una informazione più completa sull'impatto che esso ha prodotto sulla vita del genere umano.

Per risolvere il mistero riguardante l'ultimo teorema di Fermat, Pippo deve riuscire ad aprire una stanza segreta dove è contenuto un manoscritto del grande, ma un po' strano, matematico francese. Riuscite ad aiutarlo? Poca matematica e tanta logica...

La ricerca di vita su altri pianeti porta a soluzioni forse un po' troppo fantascientifiche...

Maurizio è stato velocissimo nello "scardinare" il problema. Io riporto la via forse più semplice, passando ancora una volta alle tre dimensioni.

La soluzione non era difficile e non unica. I meno esperti, però, sono stati silenti. Torniamo, quindi, a problemi un po' meno banali...
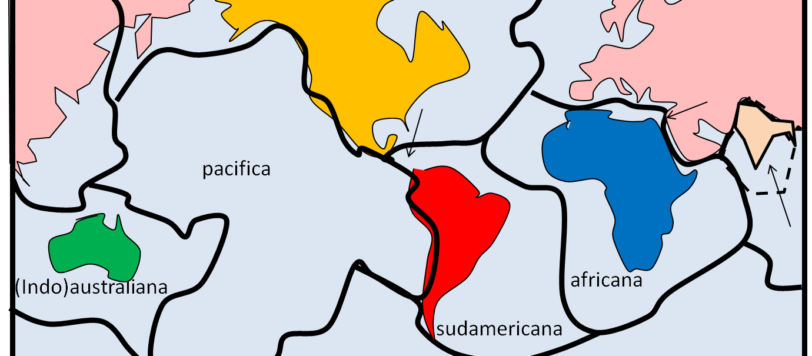
Una semplice chiacchierata sulla divisione delle terre emerse in continenti che tanto ricorda la classificazione dei corpi planetari...

In attesa di un nuovo quiz piuttosto difficile, eccone uno per i meno esperti... Invito i più bravi ad aspettare un paio di giorni. N.B.: Il quiz è stato aggiornato, imponendo il non piegamento del foglio.

L'analisi delle forme assunte dalla superficie terrestre è di importanza fondamentale per la geologia e rappresenta spesso il primo passo da compiere per formulare ipotesi sui meccanismi che le hanno generate. Il medesimo approccio può rivelarsi molto utile nell'indagare i corpi celesti solidi del sistema solare e ipotizzare modelli del loro interno. E le sorprese talvolta non mancano...

Calcoliamo tre limite notevoli che ci saranno utili per il calcolo di altre derivate. Per far ciò dobbiamo ricordare il limite che definisce il numero di Nepero e.