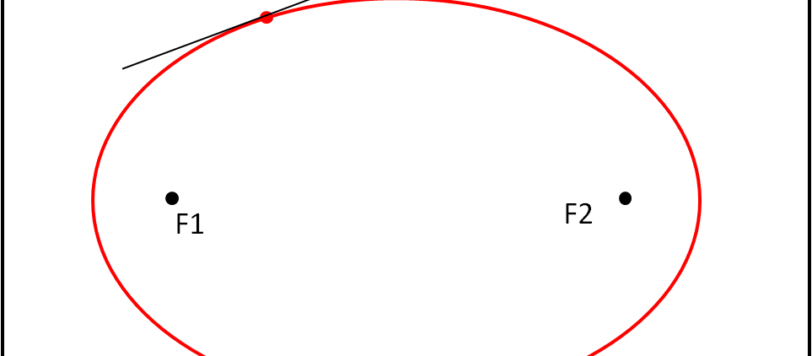
Risolto (da Leandro) il problema della costruzione della tangente all'ellisse in un punto, possiamo cominciare a giocare a biliardo su un tavolo dalla forma molto particolare: l'ellisse.


Risolto (da Leandro) il problema della costruzione della tangente all'ellisse in un punto, possiamo cominciare a giocare a biliardo su un tavolo dalla forma molto particolare: l'ellisse.
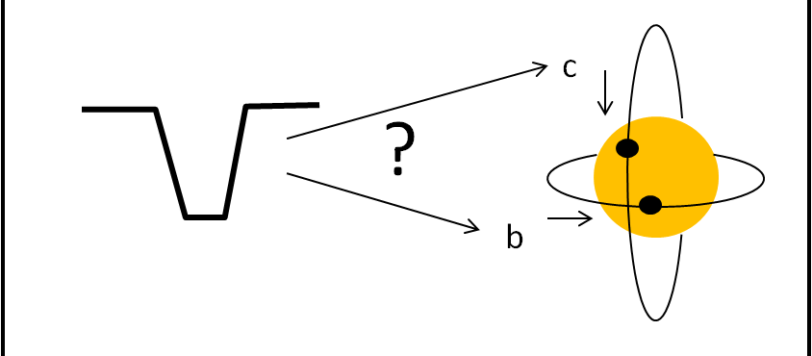
Chi pensava che i pianeti fossero figli delle stelle ubbidienti e calmi deve proprio ricredersi...
Prima di giocare con un biliardo un po' speciale, fatemi fare una domanda-quiz sicuramente non difficile.
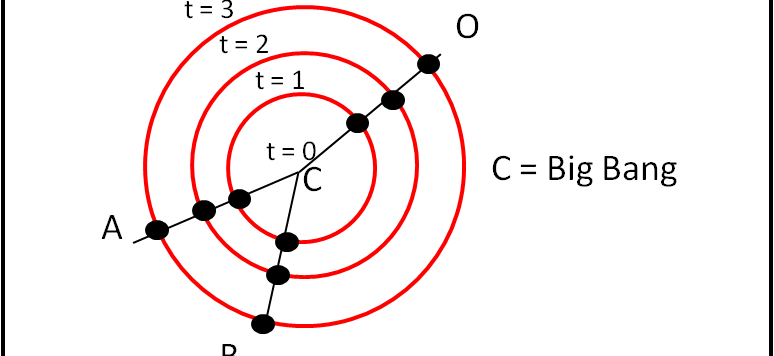
Sembra quasi impossibile, ma la solita vecchia domanda continuo a sentirla ripetere. Proviamo a rispondere in modo ultra semplice utilizzando solo un po' di geometria elementare e affidandoci a un vero superastronomo dotato di una tecnologia eccezionale. La sua risposta alla domanda sarà forse, finalmente, accettata da tutti, basandosi soltanto su dati osservativi.

Questo articolo è già stato pubblicato e lo avevamo pensato come primo di una serie basata sulla libera traduzione di alcune delle celeberrime lezioni di fisica tenute da Richard Feynman alla Cornell University dal 1961 al 1964. Ma, nel momento in cui abbiamo provato a scrivere il seguito, ci siamo resi conto che il contributo originale alla comprensione della gravità si esaurisce in questa prima parte e andare avanti con una semplice opera di traduzione delle sue lezioni (peraltro già disponibile e facilmente acquistabile anche in rete), non ci sembra avere alcun valore aggiunto per i nostri lettori.
Riproponiamo, pertanto, questo articolo per riportarlo alla vostra attenzione e aggiungere una gocciolina all'oceano della divulgazione del Feynman-pensiero. Con l'occasione, lo inseriamo in quel vaso di Pandora che è l'archivio di questo Circolo-Blog, per la precisione nella sezione dedicata alla Dinamica e Meccanica in Fisica classica.
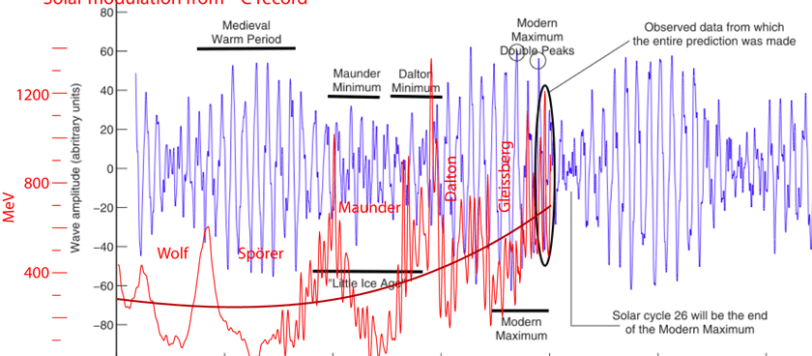
In attesa di un colloquio diretto con la prof. Zharkova, per valutare, tra l'altro, quanto la presenza di un eventuale nono pianeta possa contribuire alle anomalie da lei riscontrate in relazione alla variabilità dei minimi e massimi solari, mi sono letto attentamente i suoi studi e ciò che viene fuori: a parte l'estrema correttezza e precisione dell'analisi dei dati (cosa ben poco rispettata al giorno d'oggi), il suo lavoro è veramente fondamentale e innovativo.

Vogliamo cercare di rendere più semplice possibile il tentativo di gettare un sasso in modo che riesca ad arrivare il più lontano possibile. Per riuscirci, utilizziamo un semplice metodo basato sulla geometria e su un pizzico di fisica classica.

Riprendiamo un argomento che forse è stato trattato in un periodo in cui, giustamente, i nostri lettori potevano finalmente godersi un po' di vacanze.

I sistemi planetari hanno sicuramente un'infanzia molto nervosa e agitata e gli impatti tra corpi planetari in formazione dovrebbero essere abbastanza comuni. Come poterli osservare, direttamente o indirettamente? Nessun problema, la stella ne conserva una ... foto.
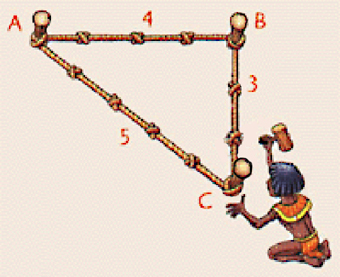
La geometria "applicata" delle prime civiltà ci stupisce sempre di più. Probabilmente, la geometria nasce addirittura prima del linguaggio, come si può evincere anche dalla disposizione di molte strutture megalitiche.
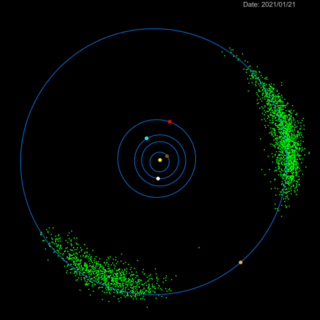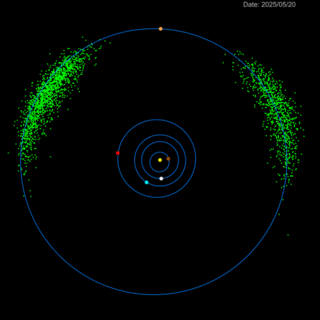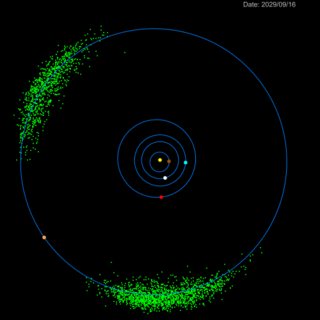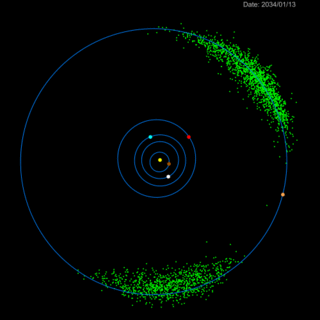
Anche se ben pochi l'hanno ricordata, la missione Lucy della NASA è partita pochi giorni fa per il suo viaggio che durerà 12 anni e che la porterà a visitare un certo numero di asteroidi troiani.