Conosciamo tutti la leggenda che riguarda Giotto e la sua “O”. Oggi siamo capaci tutti di disegnare, attraverso la tecnologia, un cerchio perfetto, una forma geometrica essenzialmente teorica. Esiste, infatti, in Natura qualcosa che sia veramente circolare o -meglio ancora- sferica? Bene, sembra che la Natura si sia data da fare e stia per raggiungere Giotto.
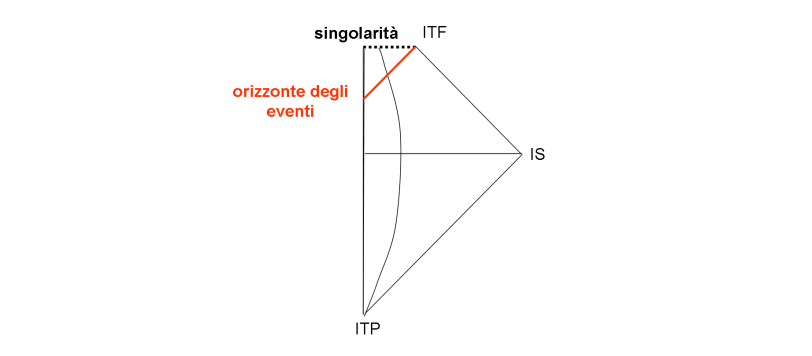
Devo ammetterlo... quando il nostro carissimo amico Frank aveva detto, con la sua irresistibile sincerità intellettuale, che non capiva come, nella consueta rappresentazione della gravità generale, simile a ciò che capita attorno a una pietra posata su un lenzuolo, potesse avvenire la caduta di un oggetto inizialmente fermo, ho cercato di girare intorno al problema, evitando di mostrare apertamente come quella figura sia esageratamente approssimativa e, in realtà, del tutto fuorviante. Può darsi che essa illuda molti di aver capito facilmente lo spaziotempo einsteniano, ma, invece, cancella una parte fondamentale dell'intera faccenda, una parte che, se trascurata, ci allontana dalla vera fantastica essenza della Relatività Generale. Con questo articolo, magari non semplicissimo, ma accessibile a tutti, vedrò di rispondere nel modo più corretto a Frank e di dare al tempo il suo giusto ruolo.
Ecco due soluzioni per la nostra capretta tosaerba molto efficiente, con la seconda trovata dal nostro instancabile Fabrizio, che ringrazio di cuore.
Gli articoli della serie "Trigonometria per tutti" sono inseriti all'interno del CORSO DI MATEMATICA Questa serie di articoli, relativi a formule trigonometriche di uso non sempre comune, ma che non è raro trovare in molte dimostrazioni, sarebbe di pura didattica. In particolare risponde all'incertezza giustificata di Franco nel quiz su Giggiriva. Tuttavia, sperando di dare […]
La tradizione vuole che si debba arrivare a comprendere il presente ripercorrendo la storia passata. Ma la discontinuità tra il modello Newtoniano, estremamente intuitivo e tangibile, e quello Einsteiniano, più generale e più lontano dalle esperienze quotidiane, è tanto più insormontabile, quanto più prolungata è la familiarità con il pensiero tradizionale.
Invece di trasmettere "certezze" superate da oltre un secolo, è necessario creare una mentalità orientata già da subito ad accogliere la corretta e più ampia visione della realtà, negli anni in cui le menti sono più ricettive ed elastiche, immuni da polarizzazioni e tabù. Forse avremo anche una società più attenta e smaliziata.
Un simpatico problema geometrico che mette in gioco i percorsi su una superficie cilindrica e che vuole dimostrare come spesso e volentieri una soluzione apparentemente immediata nasconde un approccio matematicamente più complesso. Come dire che la fretta è una cattiva consigliera.
Questo articolo compie il terzo passo verso una rappresentazione sufficientemente comprensibile dell'aspetto di una 3-sfera (immersa in un 4-spazio) in un 3-spazio, cercando sempre la massima semplicità (gli asterischi sono sempre due!). Ci troveremo di fronte l'Universo di Einstein e quello, ben più antico, di Dante Alighieri. L'inizio di una nuova avventura...
Iniziamo il nostro progetto verso l’Universo di Dante e quello di Riemann ed Einstein. La prima cosa da fare è cercare di rendere “visibile” e/o “immaginabile” un’ipersfera e lo faremo grazie all'aiuto di alcuni bacherozzi dotati di grande spirito d'osservazione e di intelligenza non comune!
Solo la presentazione di un progetto alquanto ardito, ma che non poteva mancare nel nostro Circolo: letteratura, storia e scienza a confronto e intrecciate assieme lungo un intervallo di tempo che va dal medioevo più cupo alla cosmologia più moderna.
Questo articolo recupera vecchi articoli e quiz e presenta alcuni fenomeni che fanno apparire velocità superiori a quella della luce. Non parliamo di tachioni o di neutrini o di entanglement, ma di qualcosa alla portata di chiunque. In particolare, ci dedichiamo a qualcosa che è proprio l'opposto della luce: l'ombra!
Questa pagina è inserita nell'ARCHIVIO DEL BLOG Cosa, come e quando si osserva nell'Universo La Parallasse La Geometria sferica I Sistemi di coordinate celesti Allineamenti planetari I fenomeni mutui dei satelliti di Giove Le fasi planetarie Tycho Brahe e Copernico per Galileo pari sono Il transito di Venere: come, quando e perché Storia dell'Unità […]
Questa pagina è inserita nell'ARCHIVIO DEL BLOG CORSO COMPLETO DI MATEMATICA SEZIONE AUREA, SPIRALE DI FIBONACCI E ALTRE FORME RICORRENTI NELL'UNIVERSO LE MATEMATICHE PURE E LA TEORIA DEGLI INSIEMI INFINITI DI CANTOR ANTICHI GRECI, CHE PASSIONE ! LA GEOMETRIA DELLO SPAZIO LA GEOMETRIA SFERICA LE EQUAZIONI DIFFERENZIALI L'UNIVERSO DEI NUMERI E I NUMERI PERFETTI […]
Questo lungo articolo contiene quelli relativi all'entrata dentro un buco nero, descritto attraverso la metrica di Schwarzschild. Alcune parti contengono concetti e visualizzazioni non banali, anche se sono state escluse tutte le formule matematiche. I risultati, però, sono talmente brillanti, che meritano un piccolo sforzo in più.
Questo articolo lo dovevo a un genio come Karl Schwarzschild, anche solo per il fatto di essere stato il primo a trovare una soluzione delle equazioni della relatività generale di Einstein. Inoltre, proprio la sua metrica viene utilizzata per poter descrivere ciò che capita all’interno dell’orizzonte degli eventi e dare il via ai diagrammi di Penrose (che abbiamo già introdotto). Non dimentichiamo, inoltre, che proprio la sua soluzione ha portato alla conoscenza degli attori più esotici del Teatro dell’Universo, i buchi neri. Ho dovuto limitare la descrizione alle parti maggiormente divulgabili, tralasciando le parti più “matematiche” e complesse. Spero che i concetti generali siano comunque facilmente comprensibili. Per i più esperti ho riportato i link a un paio di articoli che mi sembrano veramente completi.
Cari amici,
domani parto per la Sardegna per fare un po' di vacanze e torno il 30 settembre. Ho con me il PC, ma spero che il tempo e i luoghi fantastici mi vietino di scrivere se non qualche risposta o poco più (ma se scoprono la gravità quantistica giuro che non mancherò di avvisarvi!).
Non è che io voglia scoraggiarvi, ma la semplicità del diagramma di Penrose è solo apparente. Ricordiamoci che essa ingloba al suo interno la metrica di Schwarzschild. Inoltre, la prima reazione che si ha è quella di aver ottenuto ben poco da questa trasformazione, che mantiene solo le linee tipo luce. In realtà, invece, è più che sufficiente per poter descrivere la struttura causale dell’intero spaziotempo e trattare geometricamente buchi neri, buchi bianchi e orizzonti vari.