Questa pagina è inserita nell'ARCHIVIO DEL BLOG CORSO COMPLETO DI MATEMATICA SEZIONE AUREA, SPIRALE DI FIBONACCI E ALTRE FORME RICORRENTI NELL'UNIVERSO LE MATEMATICHE PURE E LA TEORIA DEGLI INSIEMI INFINITI DI CANTOR ANTICHI GRECI, CHE PASSIONE ! LA GEOMETRIA DELLO SPAZIO LA GEOMETRIA SFERICA LE EQUAZIONI DIFFERENZIALI L'UNIVERSO DEI NUMERI E I NUMERI PERFETTI […]

Avreste due buoni motivi per “picchiarmi”. Il primo si riferisce al metodo che vi ho consigliato di seguire per disegnare le traiettorie viste da un sistema rotante e che adesso lasceremo da parte per utilizzarne uno più rapido e facile da eseguire. Il secondo al fatto che userò di nuovo una specie di favoletta per entrare in argomento. Lo scopo è quello di dare a un gioco, apparentemente solo geometrico, un senso molto più fisico.
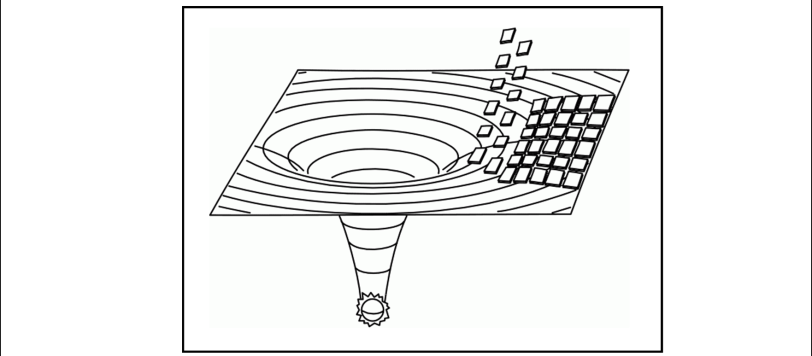
Questo articolo lo dovevo a un genio come Karl Schwarzschild, anche solo per il fatto di essere stato il primo a trovare una soluzione delle equazioni della relatività generale di Einstein. Inoltre, proprio la sua metrica viene utilizzata per poter descrivere ciò che capita all’interno dell’orizzonte degli eventi e dare il via ai diagrammi di Penrose (che abbiamo già introdotto). Non dimentichiamo, inoltre, che proprio la sua soluzione ha portato alla conoscenza degli attori più esotici del Teatro dell’Universo, i buchi neri. Ho dovuto limitare la descrizione alle parti maggiormente divulgabili, tralasciando le parti più “matematiche” e complesse. Spero che i concetti generali siano comunque facilmente comprensibili. Per i più esperti ho riportato i link a un paio di articoli che mi sembrano veramente completi.
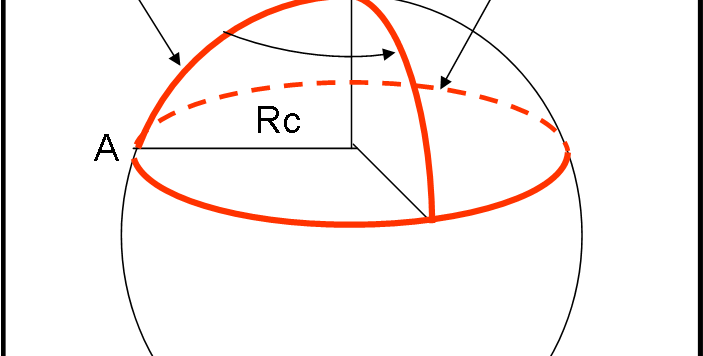
Questo articolo non contiene praticamente formule, ma è decisamente FONDAMENTALE per capire l’essenza più profonda della RG e della sua definizione di spazio tridimensionale curvo. Non perdetelo e non esitate a porre domande se vi rimane qualche dubbio. Capirete anche perché abbiamo perso tanto tempo a spiegare le regole geometriche di una superficie sferica, confrontandole con quelle euclidee e anche perché abbiamo scaldato un piano con una strana piastra. Sembrerà una trattazione addirittura pedante, ma il concetto di curvatura è troppo importante per rischiare di non chiarirlo completamente.

Abbiamo discusso a lungo della curvatura di uno spazio a due dimensioni e abbiamo visto come la geometria che lo descrive si discosti completamente da quella euclidea che impariamo a scuola. Come detto varie volte, la curvatura di uno spazio (lasciando da parte il tempo, almeno per adesso) è legata strettamente alla relatività generale, un argomento che aspetta ancora di essere affrontato in modo diretto e decisivo. Vale la pena capire ancora meglio cosa si intende per “curvatura”

Questo lungo articolo riunisce tutti quelli relativi alla geometria sferica. Esso è stato anche inserito tra gli approfondimenti.
Se la Relatività Ristretta (RR) permette di descrivere l'Universo e le leggi fisiche dei sistemi inerziali attraverso poche formule fondamentali basate su un numero ristretto di postulati, lo spaziotempo di Minkowski e il corrispondente diagramma ce ne regalano una visione grafica di grande generalità. Tutto l'Universo soggetto alla RR può essere rappresentato in un foglio di carta, utilizzando due sole coordinate. Il diagramma di Minkowski permette di comprendere appieno e di visualizzare direttamente la RR. Le sue applicazioni sono enormi e si estendono anche alla Relatività Generale.
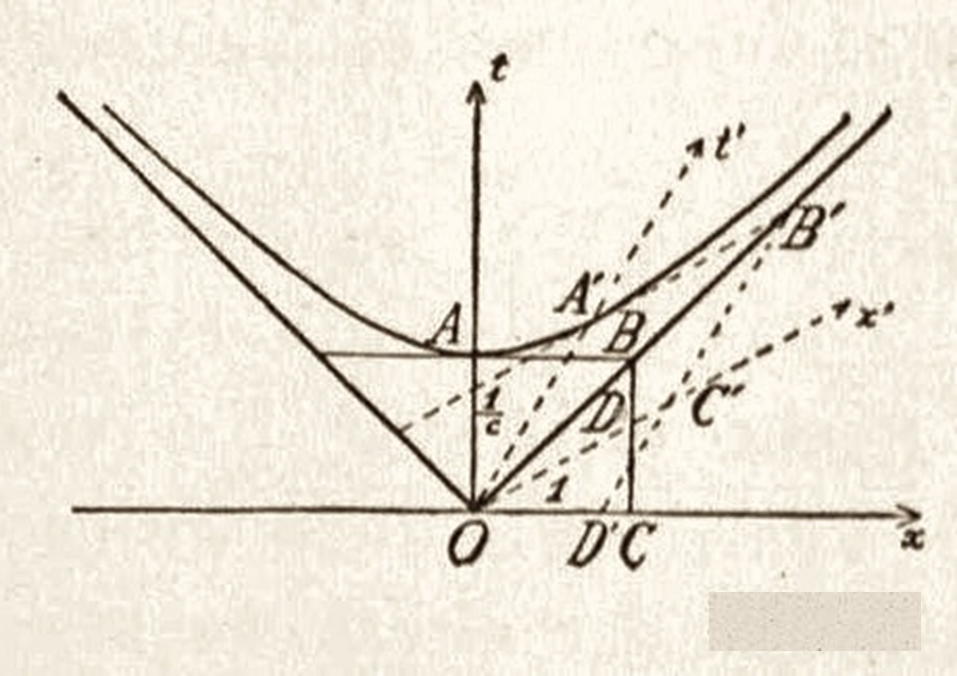
Questo quarto articolo conclude in qualche modo la presentazione del diagramma di Minkowski da un punto di vista puramente geometrico. Viene introdotto l’invariante spaziotemporale e si capisce molto meglio cosa rappresentano le iperboli trovate precedentemente. La dilatazione dei tempi segue quasi automaticamente. Tuttavia, ci fermiamo un attimo prima. L’articolo può risultare un po’ difficile se non si legge con grande attenzione e non si collega continuamente con quelli precedenti. Lo lasciamo un bel po’ in visione in attesa di domande e dubbi riguardanti “solo” lui. Mi raccomando, non cerchiamo di estrapolare in avanti se no si rischia veramente di confondere i meno preparati. Lo scopo ultimo deve essere quello di regalare a TUTTI la RR e non provare la capacità di pochi…
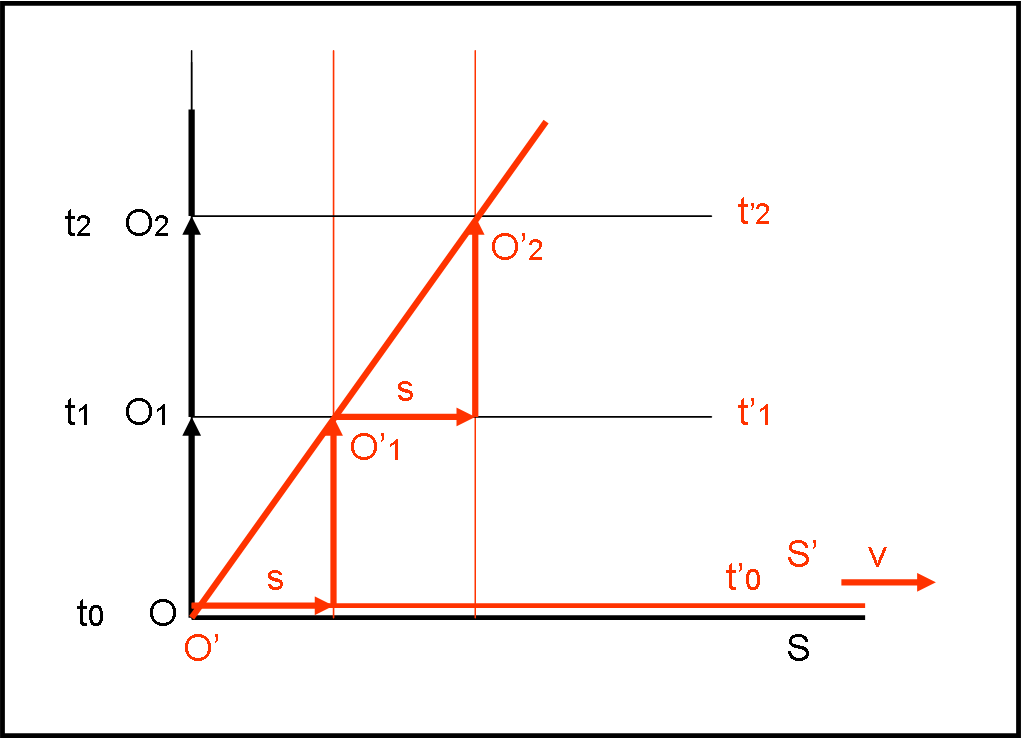
Secondo appuntamento con la RRR, forse addirittura ancora più banale e ripetitivo del primo. Tuttavia, alcuni concetti importantissimi si fanno già strada tra tante ovvietà. Uno fra tutti è la necessità di usare due orologi per misurare "qualcosa" su un altro sistema.
Questo articolo ci mostra, qualitativamente, come la relatività generale implichi una curvatura dello spaziotempo e non solo dello spazio. Purtroppo, noi intuiamo abbastanza bene solo la seconda. Limitandosi ad essa la relatività sarebbe un’assurdità. Non ci sono formule, ma il concetto non è banalissimo, benché fondamentale per immergersi veramente nella problematica dei buchi neri e non solo. Non fatevi ingannare dall’apparente banalità: se capite l’essenza del concetto di base, tutto sarà più facile.
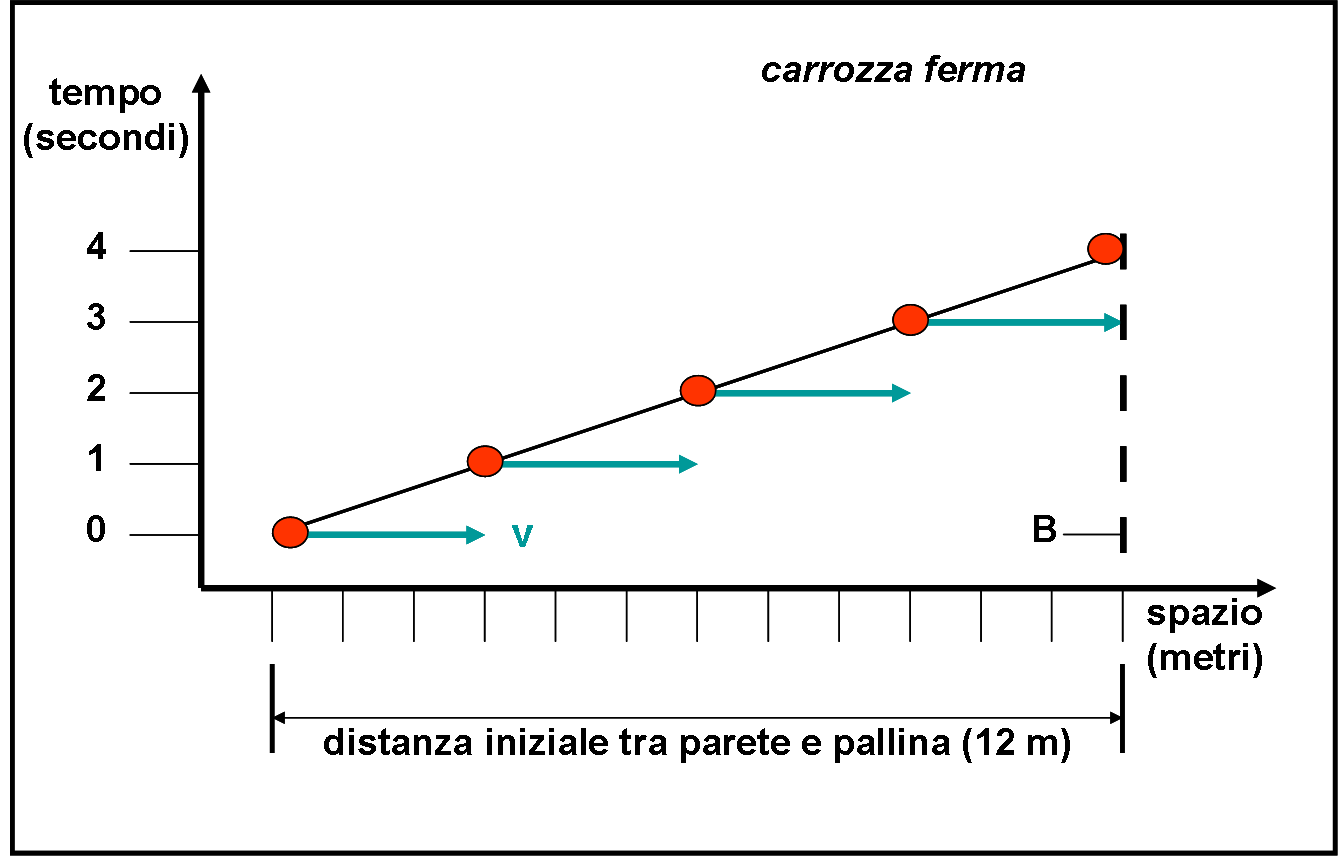
Forse non c’era bisogno di questo articolo, dato che il nostro Paolo aveva già inserito figure più che sufficienti a spiegare il fenomeno. Tuttavia, voglio ulteriormente semplificare la situazione attraverso grafici ancora più dettagliati in modo da passare, quasi senza accorgersene, da spazio a spazio-tempo. Un passaggio che non solo ci aiuta a seguire il passo fatto da Einstein, ma anche quello legato ai prossimi articoli della QED. La semplicità è sempre fondamentale.
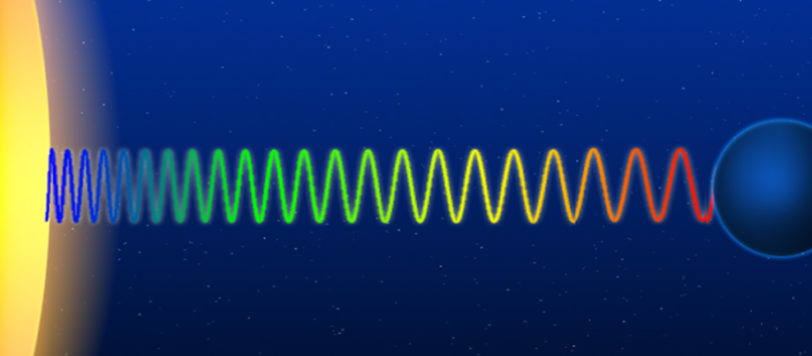
Una domanda che mi è stata fatta recentemente e che merita una risposta... Se ne potrebbero dare di diverso tipo, ma fatemi ragionare solo sfruttando la geometria dello spaziotempo.
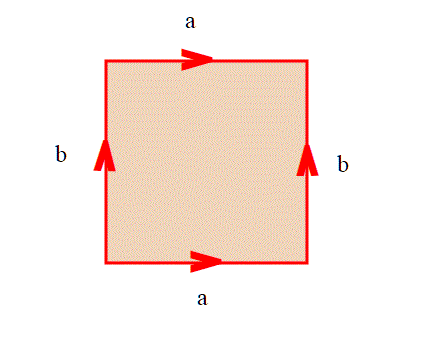
Un punto d'incontro fra il toro descritto da Arturo negli articoli sulla geometria dello spazio, e il toro "topologico" ovvero descritto in modo astratto tramite la topologia quoziente. Dimostreremo in questo articolo che le due superfici sono omeomorfe.

Due grandi matematici che, pur nella brevità della loro vita, hanno lasciato una profonda impronta nella storia della relatività.
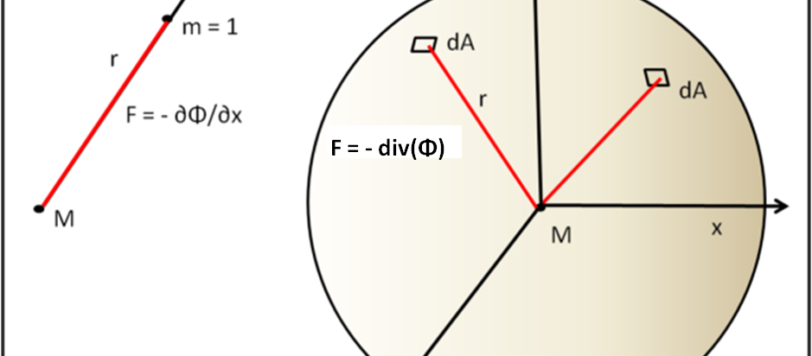
E' venuto il momento di iniziare a spostarci a destra del segno di uguale. Ci stupiremo, forse, che Einstein non annulla assolutamente la legge di Newton, ma la usa proprio per introdurre delle analogie per il caso in cui la curvatura è trascurabile. Einstein giudica Newton un grande che non poteva andare oltre e quindi prende il suo pennello e continua nell'opera d'arte ancora incompiuta. Così come Masaccio ha raccolto quello di Giotto...


