Una ciliegina facile facile... ma sempre utile.


Ho deciso di provarci ... non so quanto tempo ci metterò, dato che ultimamente mi scappa via velocemente (sarà cambiata la curvatura?). L'approccio che tra poco vi descriverò è anche legato alla richiesta di Frank che vuole sapere tutto sulle onde (non pensavo che i facoceri fossero così curiosi!). Vi sono però alcuni concetti da digerire piuttosto bene che, in questo "prologo", cercherò di mettere in luce in modo molto semplificato e generale. Forza (o -meglio- curvatura) e coraggio!

Ebbene sì... proviamo finalmente a definire in modo molto semplificato (spero) il fantomatico "tensore" che tanta paura esercita in chi cerca di avvicinarlo. Lo facciamo in modo forse meno convenzionale, cercando di affrontarlo da un punto quasi puramente geometrico, sperando che i due asterischi diano la giusta quantificazione della sua effettiva difficoltà (ossia è articolo per TUTTI coloro che si sentano di dare del tu ai vettori). Pensiamo che sarà poi più semplice capirne le proprietà che lo rendono anche un "oggetto" di pura matematica. Inoltre, cerchiamo anche di approfittare di questa introduzione per capire ancora meglio sia l'importanza e la genialità concettuale della Relatività Generale, sia la difficoltà estrema che si cela dietro una formula finale dall'apparenza molto innocua.
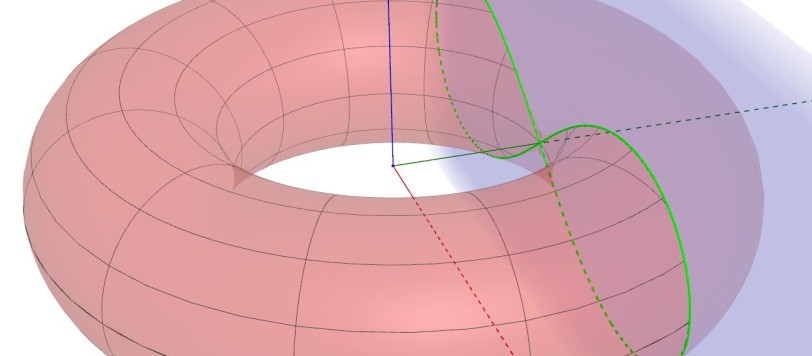
Rieccoci qui con l'ultima parte dell'appendice all'articolo 8° sulla geometria solida, dedicato al toro. Nella prima appendice abbiamo fatto la conoscenza delle circonferenze di Villarceau. In questa seconda appendice illustrerò altre interessanti curve ottenibili andando a sezionare il toro con un particolare piano. Ci serviremo, come sempre in geometria analitica dello spazio, del linguaggio della matematica. Ma niente paura, useremo strumenti semplici. E, in ogni caso, se avete dubbi, non avete che da chiedere nei commenti.
L'ultima volta avevo concluso l'articolo accennando alle sezioni spiriche, che sono proprio quelle di cui ci occupiamo questa volta. Intanto, perché si chiamano spiriche ?

Questo articolo propone un problema di meccanica classica ben conosciuto e lo affronta a livelli di difficoltà diversi. Dal moto di un sasso lungo un buco che attraversi l'intero pianeta si giunge a conoscere sempre meglio il grande genio di Newton e ci si avvicina alla curvatura dello spaziotempo. Come al solito, l'articolo finirà nell'archivio, sempre più ricco...
Questo lungo articolo contiene quelli relativi all'entrata dentro un buco nero, descritto attraverso la metrica di Schwarzschild. Alcune parti contengono concetti e visualizzazioni non banali, anche se sono state escluse tutte le formule matematiche. I risultati, però, sono talmente brillanti, che meritano un piccolo sforzo in più.

Questo articolo “cerca” di introdurre la Relatività Generale da un punto di vista abbastanza particolare, che, però, assomiglia sicuramente al carattere fanciullesco di Einstein. Un metodo saltellante e poco logico? Beh… anche in questo senso ho cercato di avvicinarmi alla formulazione di Albert, che, in fondo, non sapeva nemmeno lui cosa cercare e come cercarla. Aveva solo grandi dubbi e qualche domanda molto semplice, semplice come l’intero Universo. Un uomo vero, un figlio del Cosmo, forse il solo che parlando il suo stesso linguaggio, poteva superare un confine apparentemente insuperabile.
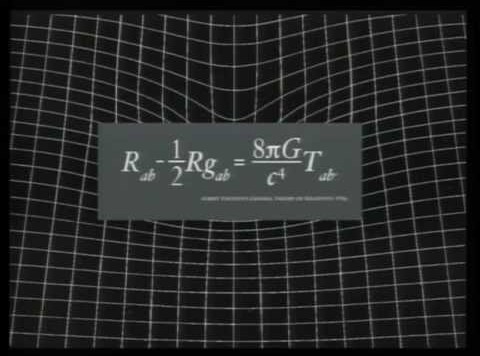
Siamo giunti alla formula risolutiva, a quella che lega curvatura con massa/energia. Curvato il tempo, dovremo affrontare una piccola lotta tra RR e RG per descrivere il moto di tutto ciò che finisce nei pressi di una massa con una densità importante. Anche la luce deve inchinarsi alla legge forse più rivoluzionaria della Scienza.
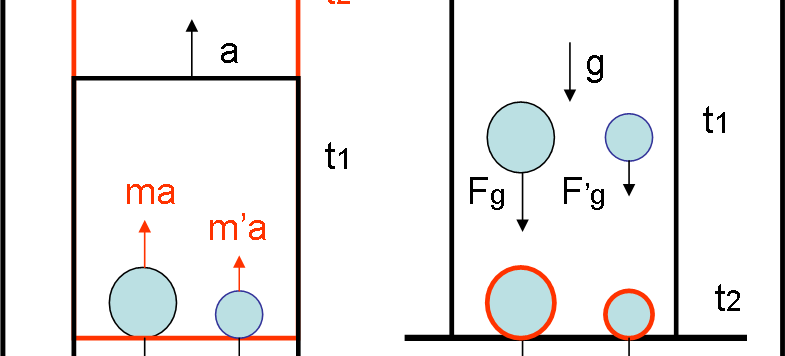
Galileo ha avuto i suoi gravi, Newton ha avuto la sua mela e Einstein ha avuto il suo … imbianchino. Ebbene sì, sembra che l’idea più straordinaria che abbia avuto Einstein (secondo le sue stesse parole) gli sia venuta parlando con un imbianchino che era caduto da un’impalcatura di fronte al suo palazzo. Dopo di allora, forze apparenti, inerzia, accelerazione, gravità hanno iniziato a cambiare completamente la loro descrizione (in pratica sono scomparse) e, allo stesso modo, le conclusioni di Galilelo e Newton sull’uguaglianza “fortunata” di massa gravitazionale e massa inerziale, è diventata l’ovvia conseguenza della gravità.
Sono appena tornato da una settimana di ferie e mi sono trovato due commenti ai quali vorrei rispondere in modo corale, soprattutto per far capire ancora meglio lo spirito del circolo (e certe sue caratteristiche) a chi lo ha seguito da poco tempo.
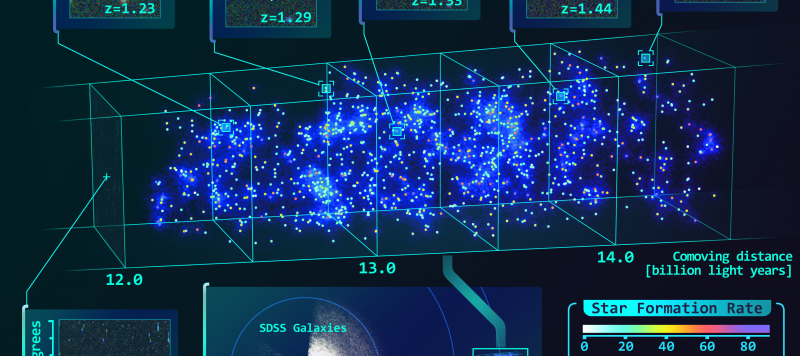
Uno straordinario lavoro di ricerca giapponese ha dimostrato, analizzando i moti delle galassie con un redshift intorno a 1.4, che, anche in queste condizioni primigenie, la teoria della relatività funziona perfettamente, a patto di conservare la famosa costante cosmologica che Einstein giudicava il suo più grande errore.
Il titolo potrebbe trarre in inganno, dato che non è stato (ancora) scoperto il gravitone. Ma poco importa… le conseguenze sono le stesse. Da domani l’uomo ha la possibilità di utilizzare un nuovo “senso” per studiare l’Universo. E’ questa la vera grandezza del rilevamento di cui siamo stati informati ieri. Chi si limita a dire che è una conferma della relatività, ne diminuisce mostruosamente l’importanza.
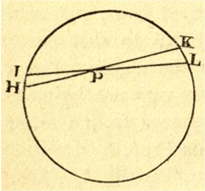
Questo articolo risponde al quiz sul buco della Terra. Ma, in realtà, va ben oltre e ci insegna a valutare sempre meglio la semplice genialità di Newton oltre che darci uno spunto per capire, ancora una volta, cosa s’intende per curvatura spaziotemporale. Questo è il bello della fisica: ogni argomento riesce a collegarsi strettamente a un altro e poco importa se siamo vicini alla Terra o in prossimità di un buco nero. Devo complimentarmi con alcuni di voi (non faccio nomi) che hanno quasi completamente risolto il problema e che, quando ci si sono avvicinati soltanto, hanno mostrato di aver compreso appieno il concetto di fondo su cui lavorare. Le leggi della fisica e la loro eleganza e generalità si imparano un po’ alla volta. Siamo tutti studenti che cerchiamo di aggiungere continuamente un mattoncino alla nostra costruzione, che, se ha le basi solide, non rischierà più di cadere.
Questo è un breve articolo a sé stante che, però, mette in evidenza un problema normalmente sottovalutato o -addirittura- dimenticato, che ha un’importanza enorme nel comprendere la differenza tra meccanica newtoniana e relatività generale. Vale la pena richiamarlo, dato che i buchi neri stanno “strapazzando” il nostro povero spazio-tempo.

Un articolo su cui ho speso parecchio tempo cercando di essere il più completo possibile. Alla fine mi sono, però, divertito e spero lo facciate anche voi.