In questo articolo, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti.
Proponiamo un metodo “antico”, ma sempre utile, per risolvere l’Equazione di Keplero. Lavoreremo per approssimazioni successive, cercando di arrivare al risultato finale (o almeno avvicinarlo il più possibile) attraverso un processo ripetitivo. Come al solito, vi prego di non “snobbare” questo articolo. Non fatelo per me, ma per Keplero…
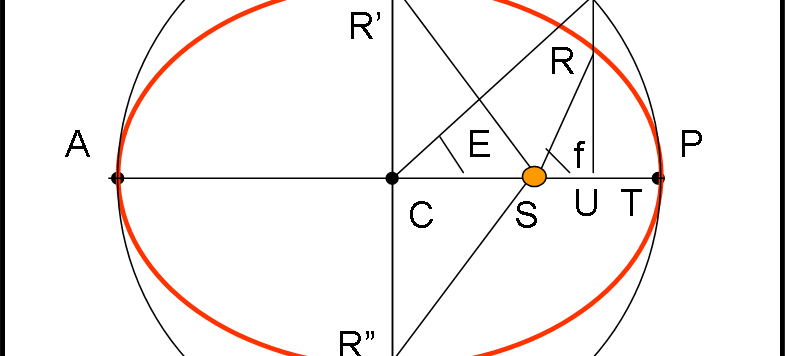
Capisco benissimo che l’argomento che andiamo a trattare possa sembrare uno di quei noiosi e inutili procedimenti geometrici e matematici. Tuttavia, vi invito a non pensarla così e a dedicargli un poco del vostro tempo. Il pensare che Keplero sia stato in parte fortunato e in parte “brutalmente” empirico nella determinazione delle sue leggi è assolutamente falso. A parte l’aver saputo sfruttare al meglio le fantastiche osservazioni di Tycho Brahe, è indubbio che solo un uomo di eccezionale intuizione e di grande capacità di sintesi poteva arrivare al risultato ottenuto. La strada a Newton non poteva essere preparata meglio.
In questa serie di articoli, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti. Nel primo di essi, parliamo di qualcosa che tutti dovrebbero conoscere: gli elementi orbitali. Tuttavia, vedremo che la determinazione degli elementi orbitali non permette di ricavare immediatamente la posizione di un pianeta nella sua orbita. La faccenda è piuttosto complicata e ha dato non pochi grattacapi allo stesso Keplero, che l’ha però affrontata e risolta con una sapienza a dir poco inaspettata per i suoi tempi.