In questo articolo, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti.
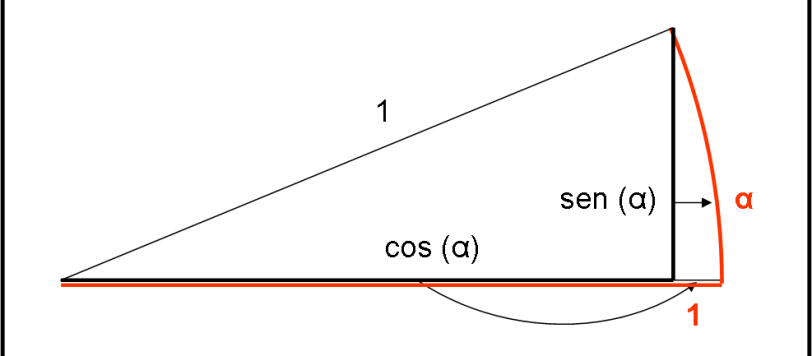
Proponiamo un metodo “antico”, ma sempre utile, per risolvere l’Equazione di Keplero. Lavoreremo per approssimazioni successive, cercando di arrivare al risultato finale (o almeno avvicinarlo il più possibile) attraverso un processo ripetitivo. Come al solito, vi prego di non “snobbare” questo articolo. Non fatelo per me, ma per Keplero…
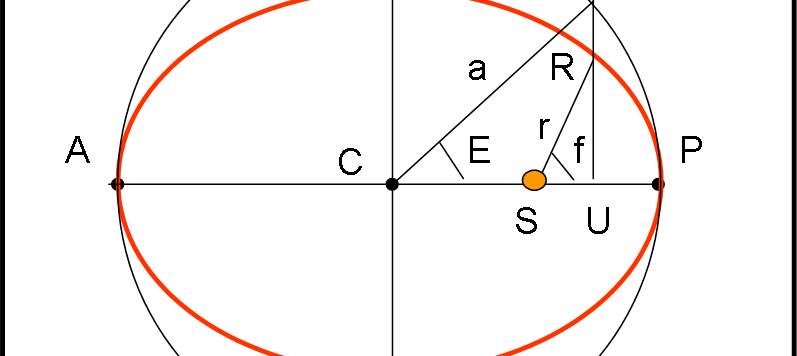
Continuiamo, seguendo Keplero, verso la sua equazione fondamentale che lega anomalia eccentrica e anomalia media. Un'equazione fondamentale che può, però, risolversi solo per approssimazioni successive, un processo, oggi, ridicolo per i calcolatori elettronici. Pensiamo, però, a Keplero che non li aveva ancora...
In questa serie di articoli, torniamo alle leggi di Keplero per definire ancora meglio le loro enormi potenzialità, specialmente se legate alla legge di Newton. Vi assicuro che sono argomenti tutt’altro che noiosi e -forse- non troppo conosciuti. Nel primo di essi, parliamo di qualcosa che tutti dovrebbero conoscere: gli elementi orbitali. Tuttavia, vedremo che la determinazione degli elementi orbitali non permette di ricavare immediatamente la posizione di un pianeta nella sua orbita. La faccenda è piuttosto complicata e ha dato non pochi grattacapi allo stesso Keplero, che l’ha però affrontata e risolta con una sapienza a dir poco inaspettata per i suoi tempi.
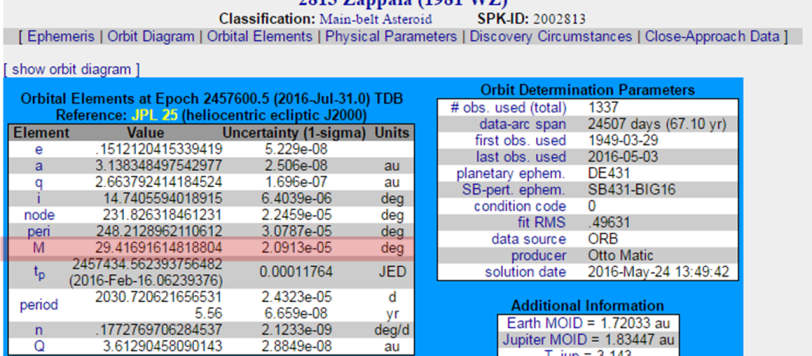
Con qualche difficoltà siamo riusciti a passare dalla legge di Newton alle leggi di Keplero. Ma abbiamo veramente analizzato a fondo le leggi di quest’ultimo? Da loro si ricavano velocità orbitale, si definiscono i parametri orbitali e si introducono nuove grandezze poco conosciute, ma di indubbia importanza culturale. Proprio una di queste ha sollevato la mia voglia di entrare nei dettagli.