Ricordando la spinta di Archimede non vi era bisogno di fare nessun calcolo...
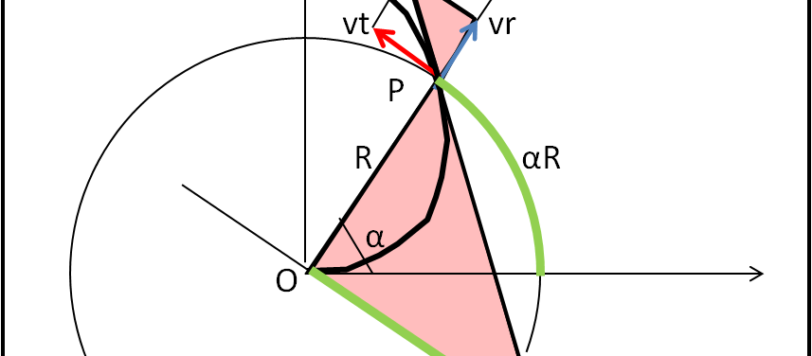
Questo articolo vuole rispondere a una precisa richiesta del nostro amico Pierluigi riguardante la dimostrazione che ha permesso ad Archimede di rettificare una circonferenza, ossia di trovare un segmento che abbia la stessa lunghezza dell'intera circonferenza
"Cos'è la matematica?" ovvero "si fa presto a dire genio" **
Un apparente paradosso di fisica classica attribuito nientemeno che ad Archimede, che sicuramente avrà utilizzato per uno dei suoi fantastici macchinari.
Dopo il coltello del calzolaio, Archimede introduce, nel lemma 14, anche la saliera (Salinon). il nome deriva sicuramente dalla forma, anche se vi sono altre ipotesi in proposito.
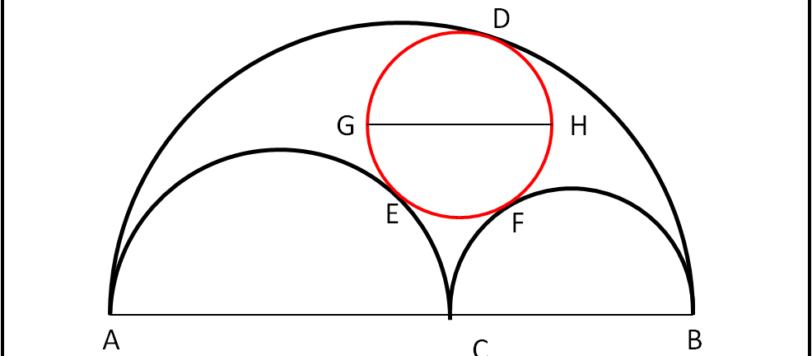
Continuiamo a divertirci con il nostro "arbelos" e a scoprire alcune delle sue innumerevoli proprietà.
Archimede ha sicuramente pensato e fatto di tutto e di più. Alcuni suoi principi sono ben conosciuti, altre sue deduzioni molto meno. Occupiamoci di loro e vedremo che Archimede può giustamente essere chiamato il "re dei cerchi".
Un classico problemino da scuole elementari che, però, sembra che nessuno in Italia sia capace di risolvere. Scusatemi... avevo promesso che non avrei più parlato di COVID, ma il troppo stroppia...
Un bel cartoncino, una bilancia ultra precisa e possiamo far meglio di Archimede!
La soluzione del quiz di Pippo e del solito Nobody. Benché sembri impossibile, a prima vista, anche al buio, il nostro eroe sarebbe capace di catturare non una ma infinite automobiline che si dirigono ognuna in una direzione diversa verso le pareti con velocità costante. Non ci riesce ricordando Archimede, ma ci riesce passando alla "spira mirabilis" di Bernoulli. La soluzione è stata soprattutto elaborata e scritta da Maurizio che ama le spirali più che il suo amico Pautasso i marroni!
Una formula forse troppo spesso dimenticata che vede una piccola lotta "storica" tra Archimede ed Erone di Alessandria (con qualche infiltrazione cinese). Richiamiamola in quanto può essere di grande aiuto per il quiz sul mostro.
Questo è il primo articolo che vuole descrivere un "principio" (che, in realtà, tale non è) conosciuto da tutti, ma che spesso viene enunciato in modo quasi automatico, senza -forse- comprendere del tutto la sua logicità e le sue sfaccettature. Sto parlando del principio di Archimede e della spinta che ogni corpo riceve verso l'alto se immerso in un fluido. Per iniziare, vediamo come dovrebbe veramente essere considerato e come la sua descrizione vada di pari passo con la prima vera prova scientifica della sfericità della Terra.
Cosa c'entra il problema che tanto ha assillato, senza successo, gli antichi e puri "geometri" amanti della riga e del compasso con gli elastomeri odierni? Leggete e lo capirete!
In questo articolo descriviamo più accuratamente il metodo di esaustione e ci dedichiamo a seguire passo passo l’approssimazione del pi greco trovata da Archimede. Una trattazione a livello di scuola media, ma utilissima anche per chi voglia capire veramente come si può arrivare a conclusioni geniali senza algebra e senza trigonometria. Un’immersione completa nella mente del grande siracusano. Riportiamo anche la soluzione della quadratura del cerchio per mezzo della cicloide e un piccolo quiz.
Sicuramente, un apporto fondamentale alla determinazione del pi greco o, se vogliamo, alla quadratura del cerchio si deve ad Archimede. Particolare importanza e suggestione ha il suo metodo meccanico a cui avevamo già accennato nell’articolo sul calcolo della superficie e del volume della sfera. Iniziamo a eseguire la quadratura di una parabola…
Tutti dovrebbero ricordare le formule che ci regalano le aree e i volumi delle forme geometriche più comuni. Ma, probabilmente, non tutti sanno come e chi è riuscito a ricavarli. In realtà, oggi vi sono metodi matematici estremamente efficaci, ma come la mettiamo per gli antichi? Eppure, anche senza integrali, derivate, trigonometria, limiti, algebra, ecc., ecc., erano già riusciti a determinarne i valori attraverso incastri geometrici di rara genialità e, soprattutto, eleganza. In particolare merita un posto d’onore il grande Archimede, l’uomo della “sfera e del cilindro”, colui che usava la leva per calcolare aree, volumi e centri di gravità.
- 1
- 2