Ovviamente l'IA mi ha fornito un risultato errato, mentre Andy ha risolto il problema in modo perfetto. Io ho seguito un metodo un po' diverso, ma ne esistono sicuramente molti altri. Basta riflettere e lasciar perdere i "saggi" consigli dell'IA. Il ragionamento di partenza è piuttosto semplice: Un triangolo è sempre circoscritto in un cerchio, […]
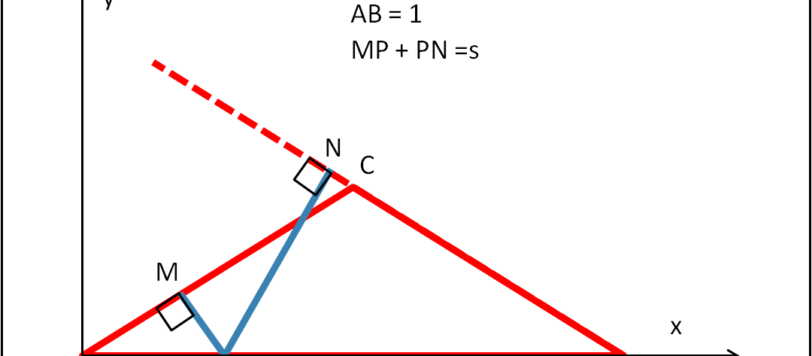
Dopo nuclei che si divertono a rompersi e a unirsi, treni che fischiamo, evoluzione cosmologica, torniamo alla cara geometria (Euclide si è un poco alterato della vostra poca passione a riguardo...).
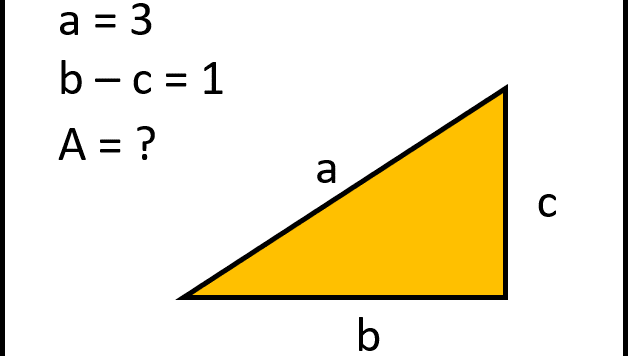
Facciamo divertire anche i meno esperti... Un povero triangolo rettangolo è sicuramente molto intelligente, ma ha appena iniziato lo studio della geometria e della matematica. Gli si fa una domanda che sembra irrisolvibile per la sua limitata preparazione. Riuscite ad aiutarlo?
Sospendiamo, brevemente, il lento percorso verso gli integrali e divertiamoci un attimo con la storia della matematica. Il nostro Paolo si è scontrato con la progressione aritmetica e ne ha dato una spiegazione che va più che bene (e che in fondo abbiamo già usato nel capitolo 40). Tuttavia, il calcolo della somma dei termini di una progressione aritmetica è stato risolto analiticamente da un bambino di dieci anni, un po’ sfaticato (non voleva eseguire troppi calcoli inutili), ma piuttosto intelligente! Parliamo di un certo Gauss, considerato il più grande matematico dei tempi moderni…
Non vi arrabbiate se vi sto trattando come dei bambini... ma in questo articolo non facciamo altro che calcolare l'area del rettangolo e poi attraverso di lei tentare con qualcosa di molto più "strano" (un triangolo). In fondo, stiamo solo imitando Archimede e non è certo un'offesa!