Ernesto (oltre che Andy, ovviamente) hanno risolto il quiz. Tuttavia, benché risolto in modo molto semplice si può ancora velocizzarlo. Basta ricordare che l'area di un triangolo è uguale a 1/2 del prodotto di un qualsiasi lato per la relativa altezza.
Torno alla mia cara geometria con un quiz estremamente semplice, che abbisogna solo di colpo c'occhio e un briciolo di intuito. Chissà che non si muovano i meno esperti? I calcoli da svolgere sono proprio alla portata di tutti!
Ho preparato un bel gruppetto di quiz, non veramente difficili, ma che abbisognano di riflessione e creatività. Che vi siano di compagnia sotto l'ombrellone o al termine di una bella escursione in montagna.
Ecco la soluzione puramente geometrica, anche se, come sempre, il risultato si poteva ottenere in modo analitico.
In attesa che Peppa faccia la sua tanto attesa ricomparsa (si sta facendo bella...), beccatevi questo quiz geometrico. Qualsiasi strategia è accettata, ma l'eleganza è sempre premiata...
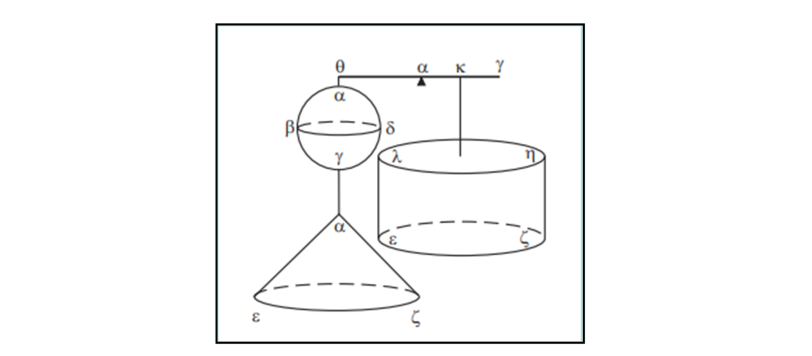
Tutti dovrebbero ricordare le formule che ci regalano le aree e i volumi delle forme geometriche più comuni. Ma, probabilmente, non tutti sanno come e chi è riuscito a ricavarli. In realtà, oggi vi sono metodi matematici estremamente efficaci, ma come la mettiamo per gli antichi? Eppure, anche senza integrali, derivate, trigonometria, limiti, algebra, ecc., ecc., erano già riusciti a determinarne i valori attraverso incastri geometrici di rara genialità e, soprattutto, eleganza. In particolare merita un posto d’onore il grande Archimede, l’uomo della “sfera e del cilindro”, colui che usava la leva per calcolare aree, volumi e centri di gravità.
Un quiz che presenta svariate soluzioni e che è stato affrontato e risolto con grande passione da almeno quattro lettori (di cui due "maghi"). Vale la pena inserire le loro strategie operative direttamente nella soluzione, ringraziando Maurizio e Scherzy per avermi aiutato in quest’opera di compattamento. Alla fine, ho aggiunto anche la soluzione scelta da me e che segue una trattazione abbastanza diversa.
Iniziamo, finalmente, il nostro lungo viaggio nel mondo degli integrali. Useremo due modi per definirli, per poi legarli strettamente attraverso un teorema fondamentale. Non abbiate paura, però: il discorso sarà molto semplice almeno fino alla “digestione” completa dei concetti più importanti. Riuscire, poi, a calcolare tutti gli integrali che si vorrebbero, diventa esercizio ben più arduo anche per i professionisti. Si usano vari “trucchi” e le serie ci aiutano. Ma… non corriamo. Cominciamo con qualcosa che è veramente alla portata di tutti: le aree dei rettangoli, dei triangoli e dei trapezi…
N.B.: i primi articoli sugli integrali sono comprensibili e utili a TUTTI, anche a coloro che non sono riusciti a seguire le tantissime lezioni sulla matematica. Vi invito perciò a leggerli ugualmente...