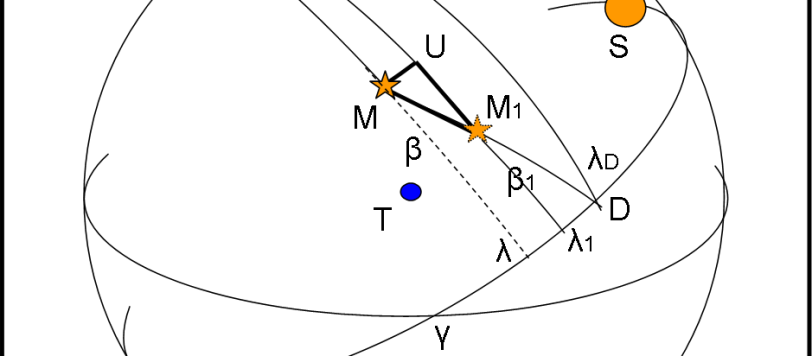
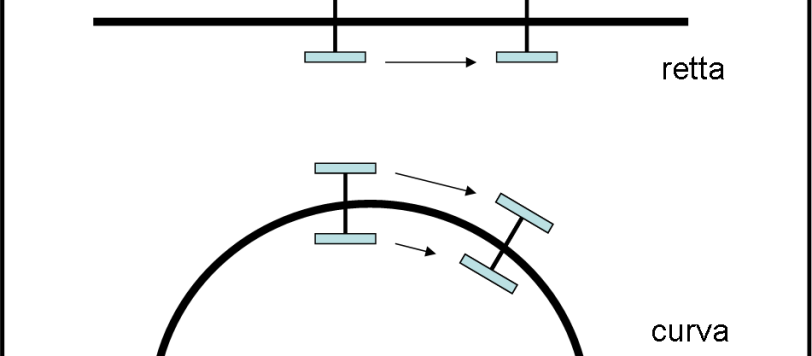
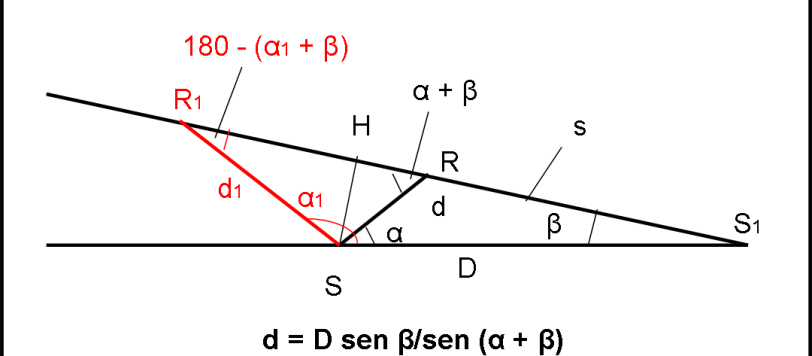
Prima di proseguire con lo studio dell’aberrazione annua e, più in generale, con i suoi effetti relativistici applicati a un astronave in volo a velocità simili a quelle della luce, cerchiamo di comprendere meglio come le ellissi apparenti si disegnino sulla sfera celeste e come si possano esprimere in termini di coordinate del quarto sistema di riferimento. Non consideratelo un discorso “noioso”…
Avere insistito a inserire nel nostro Circolo un'ampia trattazione sulla geometria sferica e sui sistemi di coordinate celesti mi sembra sempre di più un'ottima idea. Spulciando nel web e leggendo i dubbi "mostruosi" di alcuni esempi tipici di "astrofili" (e dovrebbero essere amanti del cielo...), ho capito che non solo non hanno basi scientifiche, ma non conoscono nemmeno l'ABC del loro hobby che con l'Universo e le sue leggi ha ben poco a che fare...
Questo lungo articolo riunisce tutti quelli relativi alla geometria sferica. Esso è stato anche inserito tra gli approfondimenti.
Iniziamo la nostra vita su una superficie sferica, obbligandoci a ragionare e a definire la geometria su di essa senza sfruttare la nostra capacità di osservare nelle tre dimensioni. Un impegno non sempre immediato, ma che deve essere affrontato per capire perfettamente una geometria non euclidea, la geometria che governa la sfera celeste (e anche la superficie terrestre), ma non solo. Ripeteremo, poi, gli stessi concetti usando una visione estrinseca, decisamente più comoda, ma i due metodi usati per giungere alla stessa meta daranno un quadro veramente completo della situazione
Ecco le soluzioni ai due quiz sulla costruzione del cielo visto da un’altra stella. La prima è ovvia, la seconda ha diverse possibilità. Io ho descritto quella che mi sembra più semplice, senza introdurre (ancora) teoremi trigonometrici non affrontati. Ma è solo questione di tempo… non illudetevi!