La geometria "applicata" delle prime civiltà ci stupisce sempre di più. Probabilmente, la geometria nasce addirittura prima del linguaggio, come si può evincere anche dalla disposizione di molte strutture megalitiche.
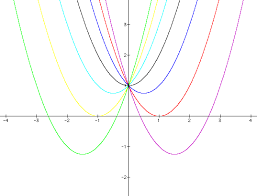
In realtà, risolvere un'equazione di secondo grado non è difficile. L'unico problema può essere, per qualcuno, ricordare a memoria la formula risolutiva. Ma è veramente necessario? Rifacendosi in parte ai babilonesi, possiamo dire di NO.
Irrazionale (non è quoziente di due numeri interi), trascendente (non può essere radice di polinomi con coefficienti razionali), non è una costante fisica, ma puramente matematica; tuttavia, sembra che non si riesca descrivere l’Universo senza di essa: entra dappertutto, dal micro al macrocosmo. E’ solo una necessità dell’uomo, che è costretto a inserirla per tentare di spiegare le leggi della Natura, o è invece un qualcosa di profondamente radicato nell’essenza stessa del Cosmo? Forse non lo sapremo mai, ma il pi greco e la sua storia sono un punto chiave di tutta la Scienza e non potevamo fare a meno di dedicargli un articolo approfondito.
E’ stato finalmente capito il significato di una tavoletta babilonese considerata a lungo misterioso. Non è altro che l’inizio del calcolo trigonometrico, risalente a circa 3700 anni fa, ben prima di quanto abbiano poi fatto i greci. Una trigonometria molto utile per costruire palazzi e templi e tracciare canali. Se si pensa cosa sta accadendo oggi in quei luoghi, mi vengono dei brividi freddi… Chissà se i cicli storici sono veramente periodici…
Stupefacente scoperta: i babilonesi utilizzavano le aree per calcolare lo spazio percorso da Giove, proprio quello che abbiamo imparato a fare nelle prime lezioni sugli integrali.