E se le ruote fossero rimaste quadrate? Poco male... bastava modificare le strade.


Nella vorticosa fucina del blog, ogni tanto succede che si producano contemporaneamente articoli gemelli, del resto anche nel mondo dei numeri esistono i “primi gemelli” e tutti ne hanno profondo rispetto. L'ultimo di questi casi riguarda la metamorfosi della catenaria in parabola, evento che è sotto i nostri occhi ogni volta che osserviamo un ponte sospeso.
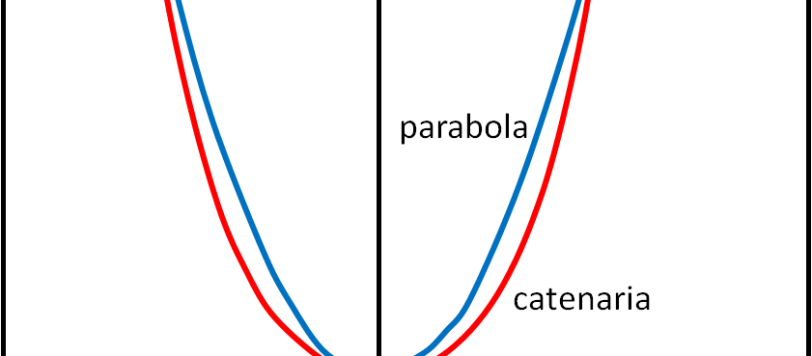
Affrontiamo lo scoglio maggiore di questa serie di articoli, ossia determiniamo l'equazione della catenaria, quella "strana" condizione di equilibrio di una catenella sospesa tra due chiodi intorno alla quale Galileo ha disquisito, accorgendosi di non essere in grado di ricavarla e accontentandosi di approssimarla a una parabola.

Prima di affrontare la determinazione analitica della curva oggi chiamata catenaria, ricordiamo come essa sia stata trattata da Galileo Galilei nei suoi Discorsi su due Nuove Scienze, senza che il grande pisano trovasse una descrizione definitiva.
Intanto , grazie a tutti coloro che hanno partecipato al quiz sulla catenaria. E' sempre un piacere vedere la gente partecipare e arrovellarsi il cervello con questi argomenti anche in pieno periodo di ferragosto Ho proposto questo quiz perché anche io, pensando ad un successivo articolo sulla catenaria, sono incappato nell'immagine che ho poi sottoposto alla […]
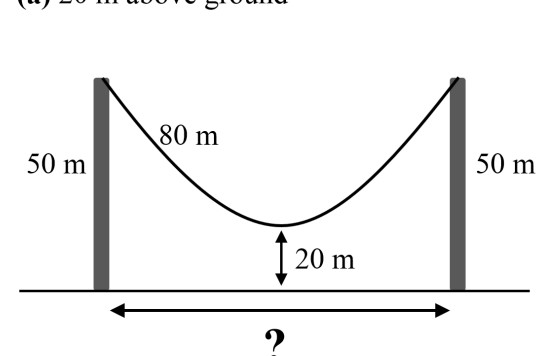
In rete si trova l'immagine allegata o altre simili a proposito di problem solving. Ma noi vogliamo scoprire qui se in tale immagine c'è qualcosa di strano. Lo scopriremo cercando di ricavare la distanza tra i i due pali. La fune è una catenaria. A voi le risposte... [19 agosto 2019: pubblicata la soluzione QUI]