Continuiamo con i nostri esercizi sul baricentro, per poi passare al momento d'inerzia e al momento angolare. Visto il silenzio, dalla prossima volta inserirò subito la soluzione. Chi vuole esercitarsi può sempre fare a meno di leggerla.
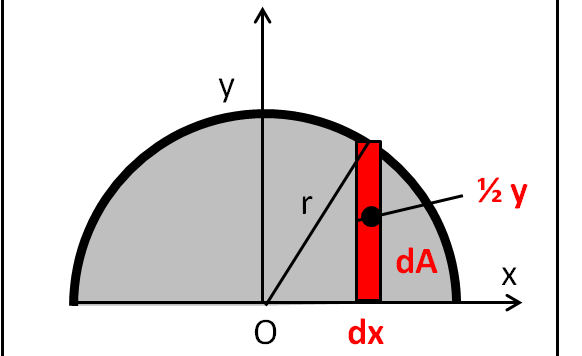

Continuiamo con i nostri esercizi sul baricentro, per poi passare al momento d'inerzia e al momento angolare. Visto il silenzio, dalla prossima volta inserirò subito la soluzione. Chi vuole esercitarsi può sempre fare a meno di leggerla.
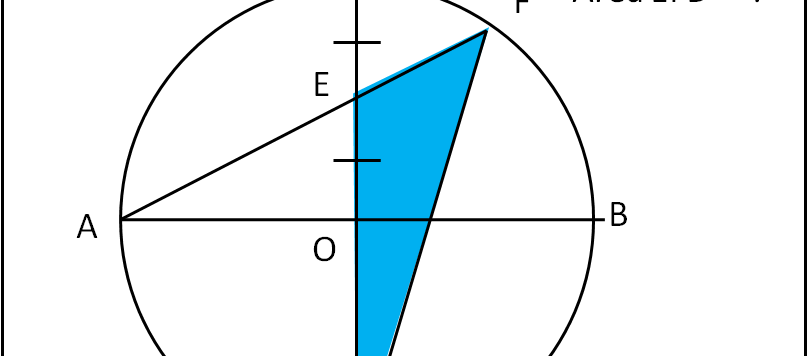
Continuo con esercizi di geometria piuttosto simpatici. In questo periodo un po' caotico non riesco a fare di più... Chi ama la geometria può trovare interessante l'ultimo commento di Andy.
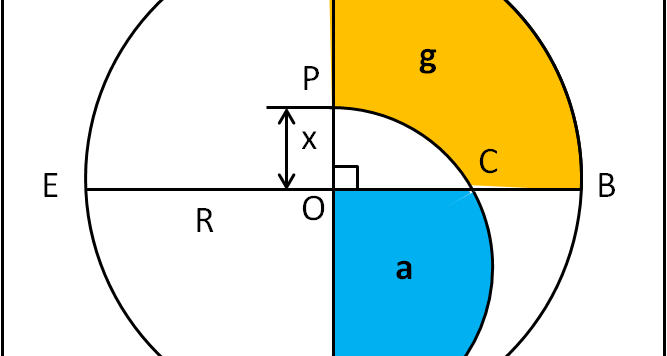
Torno alla mia cara geometria con un quiz estremamente semplice, che abbisogna solo di colpo c'occhio e un briciolo di intuito. Chissà che non si muovano i meno esperti? I calcoli da svolgere sono proprio alla portata di tutti!
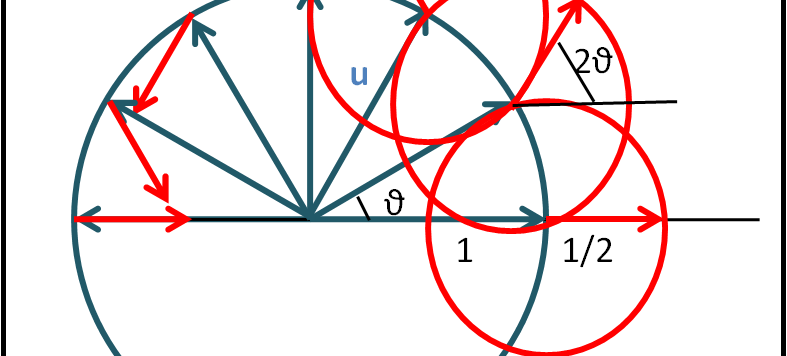
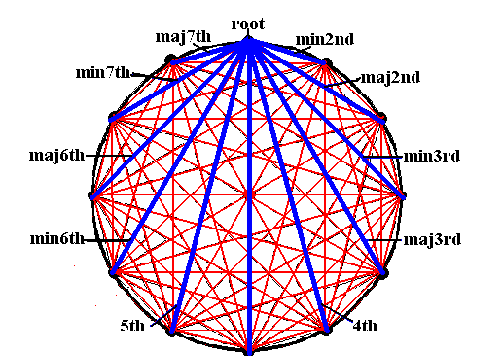
Prendiamoci un attimo di respiro e mostriamo una simpatica (e utile) visualizzazione della serie di Fourier tramite la rotazione di più vettori.
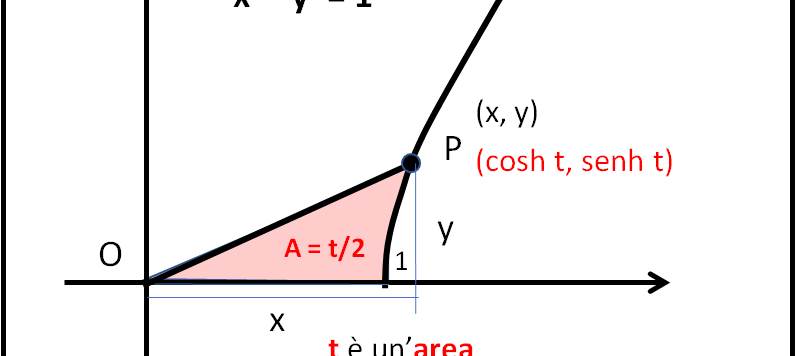
Iniziamo il nostro lungo percorso verso i ponti sospesi partendo da lontano. In particolare, dalle funzioni trigonometriche che conosciamo tutti molto bene.
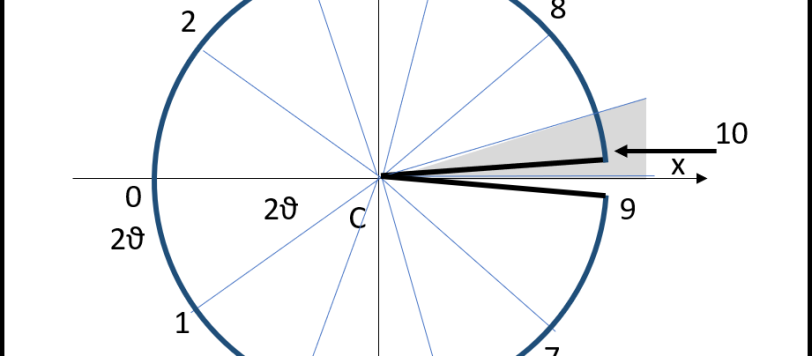
Abbiamo da poco parlato di corde (del cerchio) e di quanto possono essere utili per determinare le aree di figure curvilinee anche molto strane. Nel nostro piccolo, possiamo trovare una relazione tra due corde qualsiasi e la loro corda "media". Una formula semplicissima, all'interno di quella meravigliosa figura geometrica che è il cerchio... Ma voi potreste fare anche di più! Questa volta io mi prendo la parte più semplice e a voi "regalo" la parte più difficile.
Abbiamo visto che gli urti tra due masse e di una di loro contro una parete riesce a regalarci le cifre significative del pi greco. Analizziamo a fondo il perché, anche se Francesco ha già dato una risposta esauriente. Ci troviamo di fronte a un problema puramente matematico espresso attraverso la meccanica e dimostrabile con la semplice geometria. Un gran bell'esempio di interdisciplinarità.

Ci sono molti modi per costruire graficamente un'ellisse, ma tra i tanti proviamo a trovarne uno che ci permetterà di imitare Newton senza alcuna equazione differenziale. Un quiz che è solo l'ingresso in un mondo straordinario. Chi conosce la storia è pregato di tacere e fare pensare tutti gli altri... grazie!
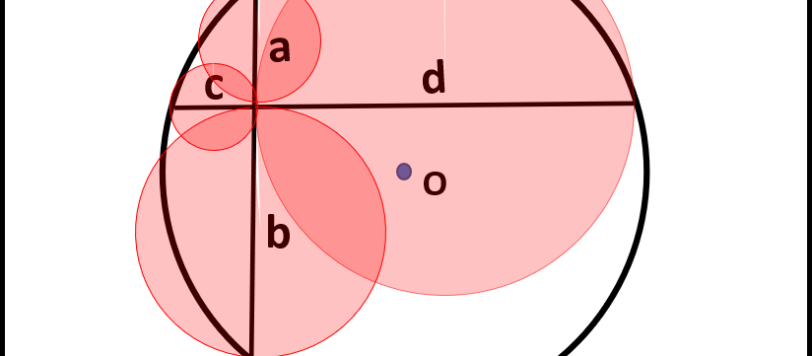
Ecco la soluzione puramente geometrica, anche se, come sempre, il risultato si poteva ottenere in modo analitico.

Questo articolo è esattamente uguale a quello precedente (terza parte) ed è, quindi, la diretta continuazione del secondo e del primo. Ho inserito all’interno le risposte alle domande che erano state fatte (tre). Per cui, posso tranquillamente eliminare quello che avevo identificato come terza parte, che viene sostituito da questo.