Due monete rotanti riescono a creare più di un paradosso che, però, possono essere risolti e/o prevenuti in qualsiasi caso, senza bisogno di formule.
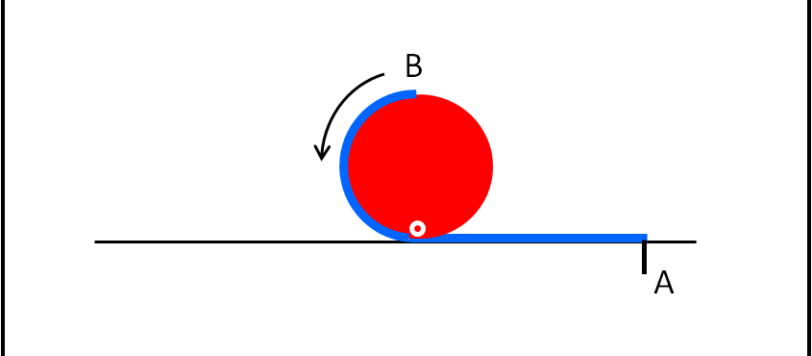

Due monete rotanti riescono a creare più di un paradosso che, però, possono essere risolti e/o prevenuti in qualsiasi caso, senza bisogno di formule.

Un premio Nobel più che giusto quello di Giorgio Parisi e fa un po' ridere che non molto tempo fa un virologo o immunologo o infettivologo, fate un po' voi, che è sempre presente in TV, lo abbia accusato, in modo più o meno trasparente, di non sapere leggere e interpretare i dati. Penso che oggi tale illustre personaggio televisivo avrebbe voluto mordersi la lingua, anche perché proprio i dati sono fondamentali per gli studi eseguiti da Parisi e che gli hanno valso il Nobel.

Questo articolo riunisce tutti quelli apparsi, relativi al "ragazzo che non amava gli integrali", ed è stato inserito nell'archivio, nella sezione matematica.
L'infinito... amore e odio degli antichi greci. Poteva essere l'insieme di un certa quantità di numeri che non finivano mai o doveva essere trattato come qualcosa di concettualmente non misurabile? Vediamo come Galileo tenta di risolvere uno dei grandi paradossi dell'antichità. Per assurdo che sembri, apre la porta al vuoto, alla caduta dei gravi nel vuoto e al calcolo infinitesimale di Newton e Leibniz.

Continuiamo a scoprire le magie di Mamikon e del suo metodo di calcolo visuale. Poi saremo pronti ad affrontare il problema della talpa aliena senza bisogno di nessuna formula che non sia quella del volume di una sfera...
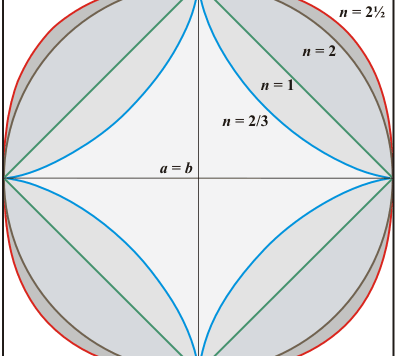
L'asteroide, o astroide, così chiamato perché la sua forma evoca quella di un astro, può essere descritto mediante equazioni parametriche ma, come vedremo, anche in altre forme. E' anche chiamato ipocicloide perché lo si può ottenere, analogamente alla cicloide, facendo rotolare una circonferenza, in questo caso non lungo una retta, ma a contatto con l'interno di una circonferenza di raggio maggiore.

Abbiamo visto come un triangolo equilatero, appeso per un vertice, possa funzionare da bilancia. Ma se la volessimo davvero realizzare fisicamente, per pesare oggetti di pochi grammi, dovremmo dotare questa bilancia di una scala di lettura che indichi i grammi da zero alla portata massima, che possiamo fissare a 10 grammi. Possiamo decidere che questo sia anche il peso del nostro triangolo equilatero che fungerà da bilancia.
La soluzione del quiz sulla catastrofe terrestre, ha innescato una trattazione ben più articolata del previsto. Su suggerimento dell'onnipresente e onniveggente Daniela, si è convenuto di associare questo articolo a quello più vecchio sul blocco della rotazione di Papalla. Il titolo unico è diventato: Fermate il mondo, voglio scendere... L'articolo è stato scritto a quattro mani e cinque teste, dato che, anche se non compare tra gli autori, la supervisione di Umberto è stata essenziale.
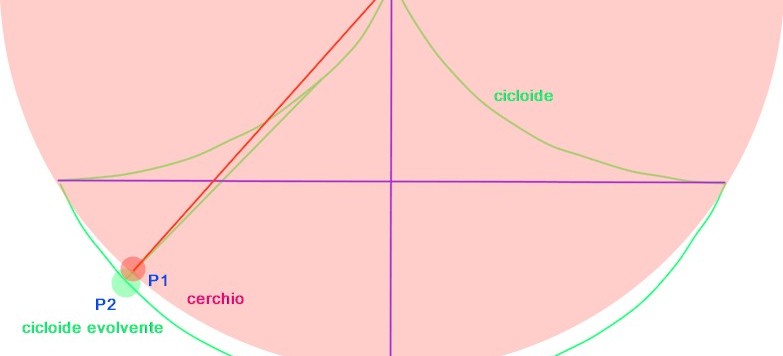
Tre secoli e mezzo fa, Christian Huygens pubblicava quello che può essere considerato il suo capolavoro: Horologium Oscillatorium, un'opera che assieme al Discorso sulle due nuove scienze di Galileo e ai Principa Mathematica di Newton, rientra fra i tre lavori scientifici più rilevanti del 17°secolo.
Nell'Horologium Oscillatorium si parla,tra molte altre cose, di orologi a pendolo e di cicloidi. Perché, Huygens, aveva capito che solo affidandosi al particolare profilo della cicloide si sarebbe riusciti ad ottenere una traiettoria migliore di quella circolare per il movimento del pendolo.

I numeri interi e i loro multipli, interpretati come onde che si propagano verso l'infinito; un modo inconsueto di riflettere sulle proprietà dei numeri interi consecutivi entro un intervallo di valori, il tentativo di capire cosa accade lontano studiando ciò che è vicino. Una specie di surfing sulla cresta delle onde, sul loro affastellarsi, morire e rinascere.

In questo articolo descriviamo più accuratamente il metodo di esaustione e ci dedichiamo a seguire passo passo l’approssimazione del pi greco trovata da Archimede. Una trattazione a livello di scuola media, ma utilissima anche per chi voglia capire veramente come si può arrivare a conclusioni geniali senza algebra e senza trigonometria. Un’immersione completa nella mente del grande siracusano. Riportiamo anche la soluzione della quadratura del cerchio per mezzo della cicloide e un piccolo quiz.

Achille ha fatto la scelta giusta, rinunciando a sfidare la Tartaruga per avere la rivincita , l'ipotesi di scendere lungo il piano inclinato nella speranza di impiegare meno tempo di quello della tartaruga, lungo la cicloide, era assolutamente da scartare.

La rabbia , l'orgoglio e la forza della ragione!
Dopo avere in parte sfogato l'ira funesta prendendo a calci lo slittino, Achille si mise a riflettere sui fatti della giornata.
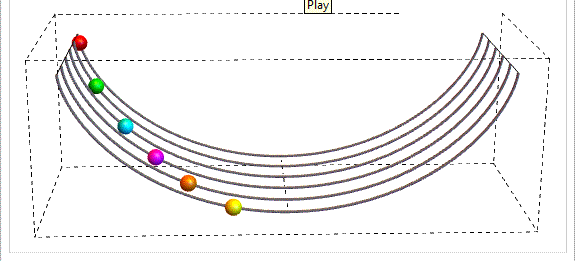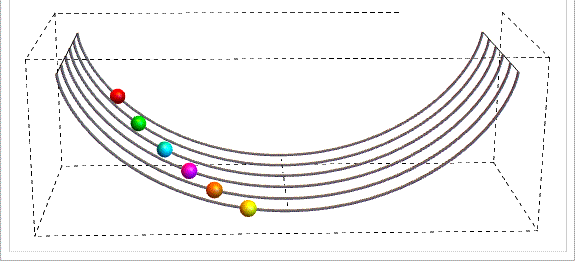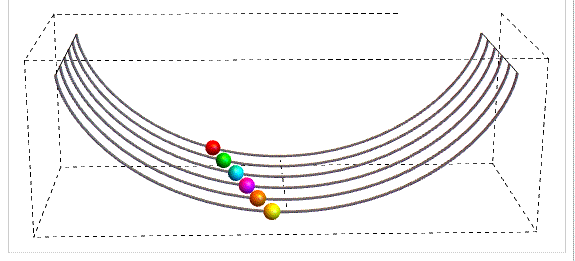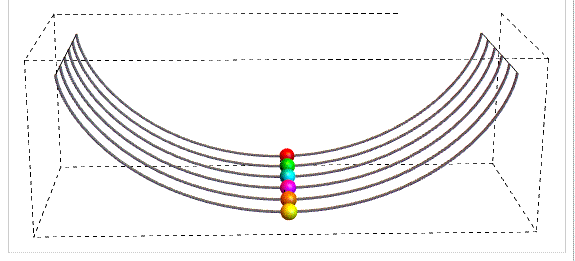
Sostanzialmente il quiz richiedeva di trovare l' equazione che rappresenta il profilo di un curva sulla quale, indipendentemente dalla posizione di partenza, il periodo delle oscillazioni di oggetti in movimento è costante.