Una soluzione tecnologica di estrema semplicità ha permesso di far correre i treni su due stretti binari senza farli deragliare, soprattutto in curva. Vediamo di descriverla in modo puramente geometrico.
Bravi Leandro e Andy nell'essere stati capaci di "vedere" in tre dimensioni.
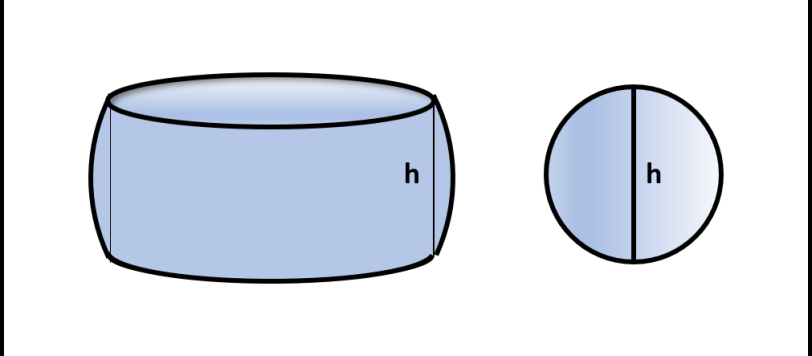
In questo ultimo articolo riguardo a Mamikon risolviamo, con il solo "calcolo visuale" , il problema relativo alla talpa spaziale. Possiamo dire di avere introdotto il teorema di Mamikon ... tridimensionale!
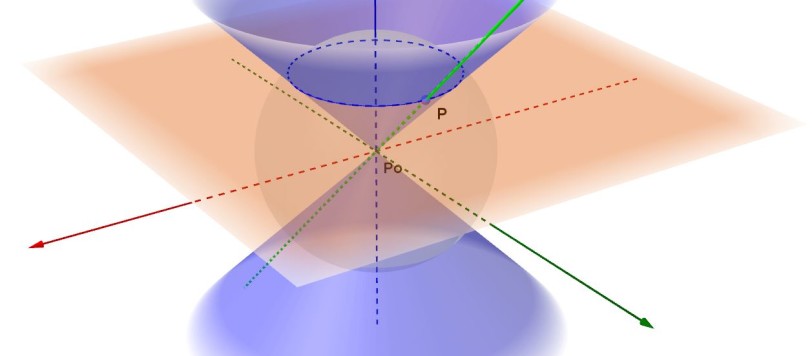
Nel mio precedente articolo ho cercato di spiegare cosa siano in geometria dello spazio le superfici di rotazione e un metodo per determinarne la rappresentazione analitica. In questo articolo fornirò una prima serie di esempi, più semplici, utilizzando ancora la possibilità di visualizzazione tridimensionale anche attraverso l'uso di occhiali anaglifici. Rammento per comodità che una […]
Questo articolo è esattamente uguale a quello precedente (terza parte) ed è, quindi, la diretta continuazione del secondo e del primo. Ho inserito all’interno le risposte alle domande che erano state fatte (tre). Per cui, posso tranquillamente eliminare quello che avevo identificato come terza parte, che viene sostituito da questo.
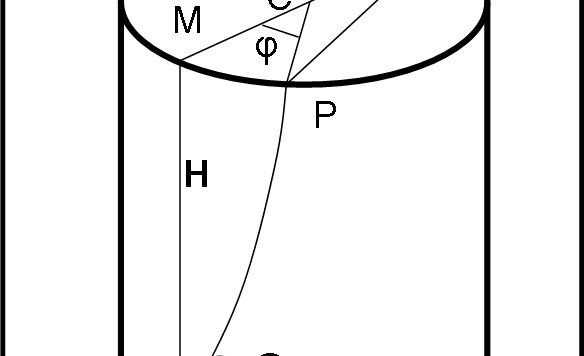
La prima parte del quiz portava facilmente a valutare due casi estremi e il tutto sembrava piuttosto semplice. La fretta, però, è cattiva consigliera ed è necessario che la formica ragioni un po’ più a fondo sulla questione (e non solo lei). Questo articolo regala la soluzione più ovvia, ma introduce un problema più complesso.
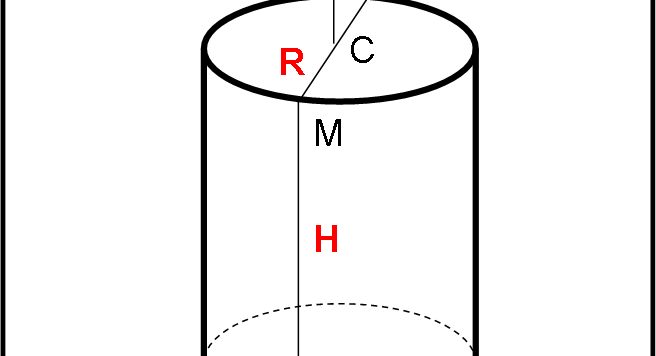
Questa prima parte del quiz è di una difficoltà molto moderata. Invito a risolverlo in modo molto rapido. Se tutto va come prevedo, avremo da discutere parecchio quando apriremo la seconda parte.
Anche questo quiz è stato brillantemente e velocemente risolto. In qualche modo, il succo di tutto è ottenere un numero dispari di litri…