Ricominciamo da... tre. Occupiamoci un po' della fisica classica e, in particolare, della meccanica, iniziando col ricavare le formule base della cinematica e risolvendo un primo esercizio.
Il linguaggio usato da Galileo per descrivere la caduta dei gravi o il moto di un grave al quale è stata impartita una certa velocità è diverso dal linguaggio usato da Newton per descrivere la "sua" forza di gravità? Sì oppure no? Discutiamone giocando con proiettili, missili intercontinentali e sonde spaziali.
Il linguaggio usato da Galileo per descrivere la caduta dei gravi o il moto di un grave al quale è stata impartita una certa velocità è diverso dal linguaggio usato da Newton per descrivere la "sua" forza di gravità? Sì oppure no? Discutiamone giocando con proiettili, missili intercontinentali e sonde spaziali.
In questo articolo analizzerò un particolare tipo di strutture, ovvero quelle basate sul principio della "tensegrity": un sistema di componenti tra loro isolati e tenuti insieme in equilibrio all'interno di una rete di elementi tesi. Il termine anglosassone "tensegrity", infatti, proviene dall'unione delle due parole inglesi "tension" (tensione) e "integrity" (integrità).
La soluzione che propongo io è sicuramente molto lunga, ma ha lo scopo di richiamare molti concetti importanti del moto parabolico.
In attesa di unire domanda e risposta sotto un unico articolo didattico che arricchirà l'archivio nella categoria Fisica Classica, ecco la soluzione del quiz di cinematica rettilinea, di tale semplicità che sia Arturo che Marco hanno solo dato un aiutino, sperando in qualche nuovo temerario.
Sapete come sono fatto… ogni tanto mi sorgono dei dubbi sulle varie spiegazioni e temo che si possa creare qualche malinteso. Probabilmente è una mia paura infondata e nessuno ha bisogno di questo chiarimento. Al limite trascurate questo articolo (ne sarei, in fondo, ben lieto).
Un problemino, senza derivate o integrali, che può sicuramente essere risolto in vari modi. Io ho scelto la soluzione che mi appariva più elegante e rapida (da cui i tre asterischi), ma ... qualcuno potrebbe sicuramente superarmi, trovando anche un procedimento più semplice. L'esercizio è stato proposto all'Università di Dublino (ma non tratta di birra...) e lo inserisco per far divertire, almeno, il nostro caro amico Arturo.
Tra topologia e relatività stiamo volando un po' troppo in alto e mi sembra giusto accontentare anche i meno esperti con qualche semplice esercizio di meccanica classica. Iniziamo con la cinematica e con un esercizio veramente banale che si può risolvere anche sotto un ombrellone.
Un piccolo problema di cinematica classica che introduce alcune formule relativamente poco usate.
Sì, lo so... vi sto tartassando con varie configurazioni nello spaziotempo di Minkowski, quando intorno a noi tutto viaggia a velocità ben minore di quella della luce... Torniamo a Galileo, cercando di agire come facciamo con Minkowski. Viva la grafica!
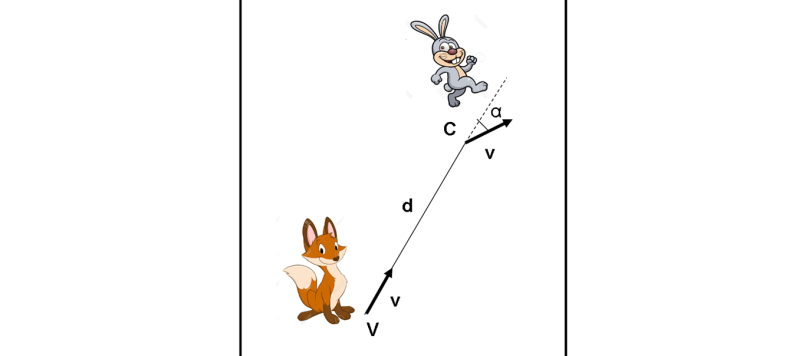
Un simpatico esercizio di cinematica, che ci porta velocemente nel mondo delle spirali che tanta importanza hanno per l'Universo. Noi ci limitiamo, per il momento, a una volpe e a un coniglio...
Il quiz sul bicchiere pieno d’acqua bucato è stato ormai risolto brillantemente da più di un lettore (primo fra tutti Pippo). Invece di dare la risposta ufficiale, descrivo due altri problemini che sono strettamente legati alla “causa” che non fa uscire l’acqua dal bicchiere bucato.
Sarebbe quasi inutile riportare la soluzione del quiz di Ulisse, dato che tante sono state le risposte esatte (era facile però…). Tuttavia, per completezza, ripeto velocemente i passaggi necessari per risolvere il problemino.
Finalmente richiamiamo i vettori e le loro caratteristiche. Siamo sempre nel campo della cinematica e, quindi, non c’è bisogno di energia. Rileggetevi i primi capitoli sul momento angolare…
Un celebre personaggio del mitico Carosello introduce un quesito estremamente facile. Chi va più veloce, un uomo o la sua ombra? Questo quiz può essere veramente risolto da tutti e mi aspetto molte risposte dai meno esperti (i più bravi stiano zitti per un paio di giorni…). Prima o poi toccherà anche a loro (ne ho preparato uno niente male…).