Trattiamo il caso in cui le due circonferenze sono una interna all'altra: le iperboli diventano ellissi.
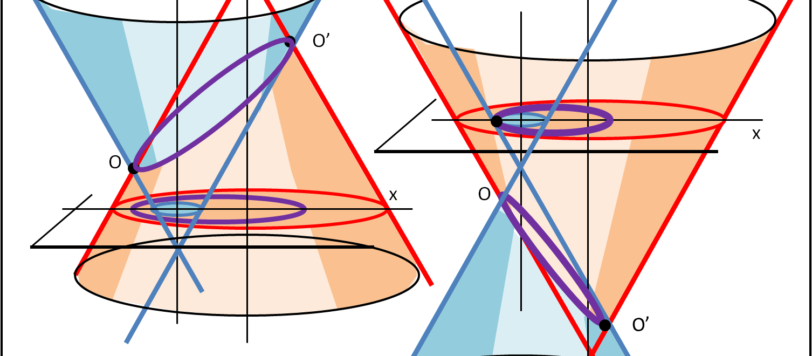

Trattiamo il caso in cui le due circonferenze sono una interna all'altra: le iperboli diventano ellissi.

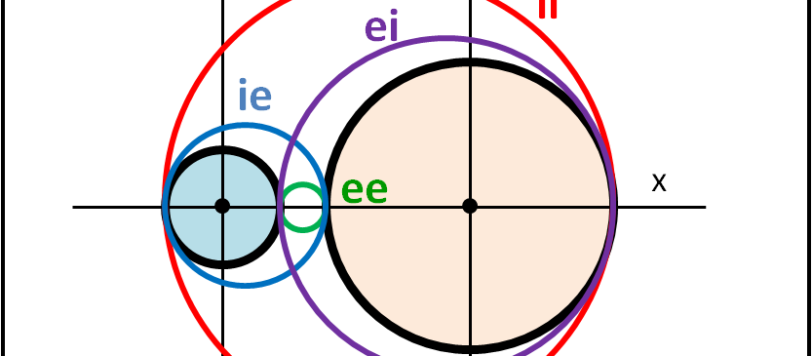
continuiamo a tracciare i centri delle circonferenze tangenti a quelle di partenza, rimanendo sempre nel caso che queste ultime siano esterne una all'altra.
Vi invito caldamente a seguire il problema la cui soluzione inizia con questo articolo. Stiamo parlando del celebre Problema di Apollonio, relativo alle circonferenze tangenti a tre circonferenze qualsiasi complanari. Non demordete, dato che Apollonio ha creato un vero capolavoro!

I giapponesi, oltre a tutti i loro misteri, i loro riti, le loro cerimonie, il loro modo di pensare e agire, ben diverso da quello occidentale, ci hanno anche regalato una geometria del tutto speciale, veramente affascinante. Iniziamo a entrare in questo mondo, dove intendo tornare spesso ...