Sappiamo molto bene che nella relatività speciale basta cambiare sistema di riferimento e se si guarda qualcosa che sta viaggiando a grande velocità il suo tempo si dilata e la sua lunghezza si accorcia. Ma è anche possibile vederla ruotare?
Vediamo di riassumere il paradosso sollevato da Pippo e poi di risolverlo applicando correttamente la relatività ristretta.
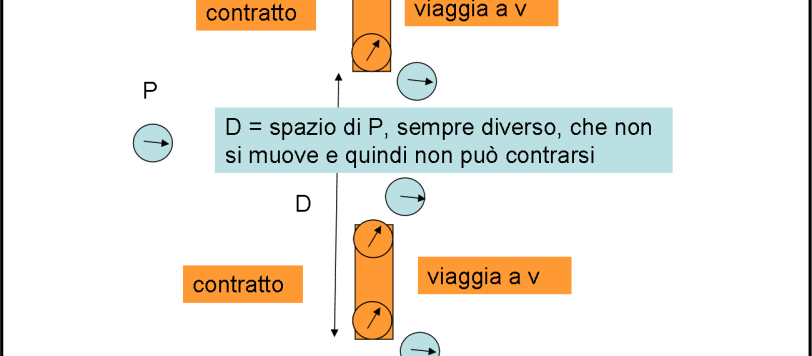
Volevo lasciar perdere dato che la nostra corda sta proprio rompendo oltre che rompersi… Tuttavia, vorrei descrivere meglio la mia visione del paradosso, decisamente semplificato rispetto a quello originario. Devo poi ammettere di aver fatto un grave errore che non avevo analizzato per faciloneria. Se ne era accorta però Dany e le devo una giusta correzione. Il succo, comunque, non cambia, fatta la dovuta variazione, e ammetto che la mia sia una visione abbastanza personale e invito tutti a distruggerla senza passare a nessun sistema in movimento, ma rimanendo in quello del papallo. Sono prontissimo ad accettare le critiche e ad abbassare la “cresta”. Non parliamo, però, di accelerazioni o di altri sistemi di riferimento…
La risposta praticamente immediata di Paolo a questo quiz ha risolto brillantemente il paradosso (e vi assicuro che non era cosa facile, pur conoscendo la RR (Relatività Ristretta). A questo punto, sembra più che giusto riportare la soluzione più generale possibile attraverso qualche formula. Non spaventiamoci: abbiamo a che fare con il solito fattore di contrazione di Lorentz e con un po’ di geometria (e fisica classica) veramente elementari, alla portata di chiunque. L’importante è riuscire a comprendere bene i concetti e seguire attentamente il ragionamento generale. Questo articolo è decisamente istruttivo per comprendere appieno la RR e può essere compreso, a livello concettuale, anche saltando i vari passaggi matematici.
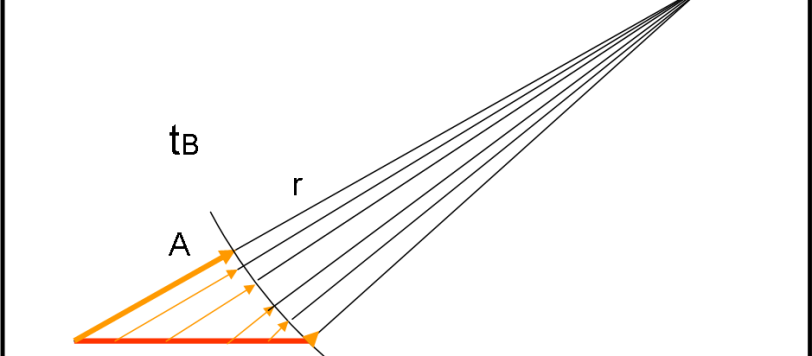
Per una analisi completa delle "Visioni relativistiche" si consiglia di leggere il relativo approfondimento, del quale questo articolo è parte integrante. QUESTO il quiz di cui questo articolo costituisce la soluzione Premessa (per i meno esperti) I fotoni sono le particelle-non particelle che trasportano la luce e riescono a esistere solo viaggiando alla […]
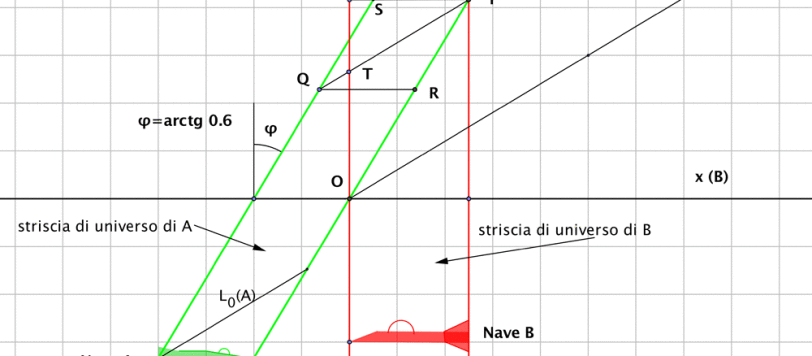
Una soluzione numerica del problema del missile, preparato da Pippo con l'aiuto di Umberto...
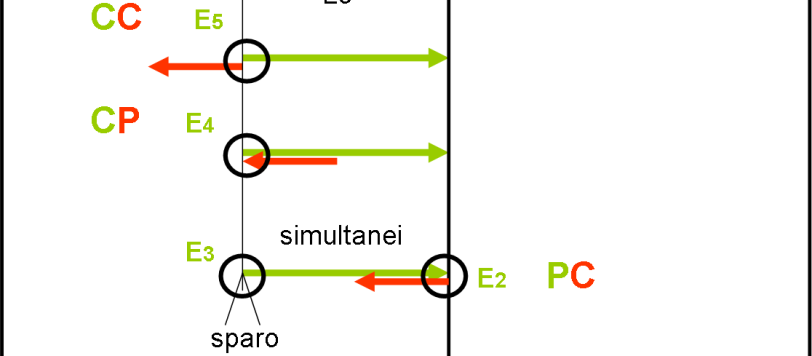
Il problema che abbiamo posto è uno dei tanti che sembrano portare a un paradosso della relatività ristretta. Il punto chiave è che tutto è perfettamente simmetrico, tranne il fatto che una certa azione viene eseguita, a un certo istante, da una sola delle due astronavi (ossia da uno solo dei due sistemi di riferimento). Ancora una volta, ci scontriamo con il concetto fondamentale della relatività della simultaneità. L’astronave A spara quando succede qualcosa (simultaneità), ma la stessa simultaneità non viene vista dall’altro sistema, dove non avviene l’evento “sparo”. Per questo articolo mi sono avvalso della fattiva collaborazione di Daniela, Paolo, Pippo e Umberto. Speriamo di aver raggiunto una chiarezza divulgativa sufficiente. Chi avesse ancora dubbi, lo dica subito. La Relatività Ristretta sa essere molto subdola…
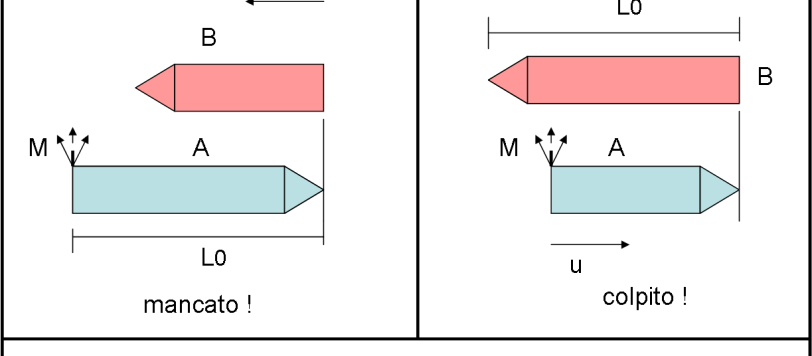
Un bel problemino relativistico (RR) che sembra portare a un paradosso. Un’attenta analisi dei fatti, però, fa rientrare tutto nelle regole… Einstein , per questa volta, si salva. Io lo giudico abbastanza difficile (rispetto a quello della volta scorsa). A voi smentirmi, come fate di solito!
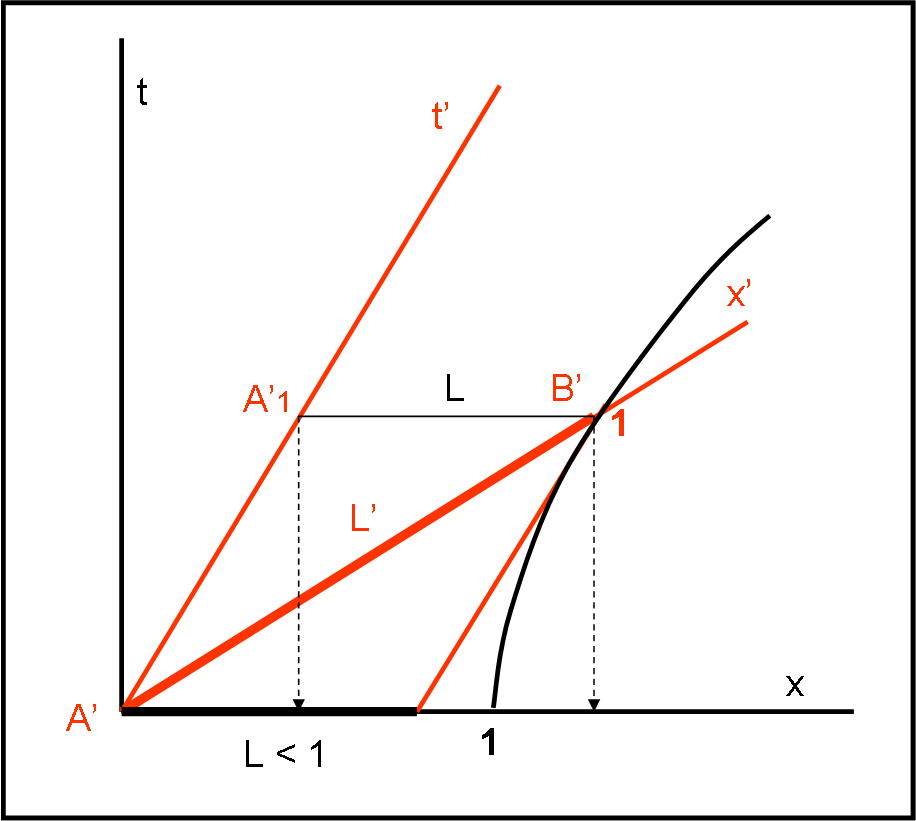
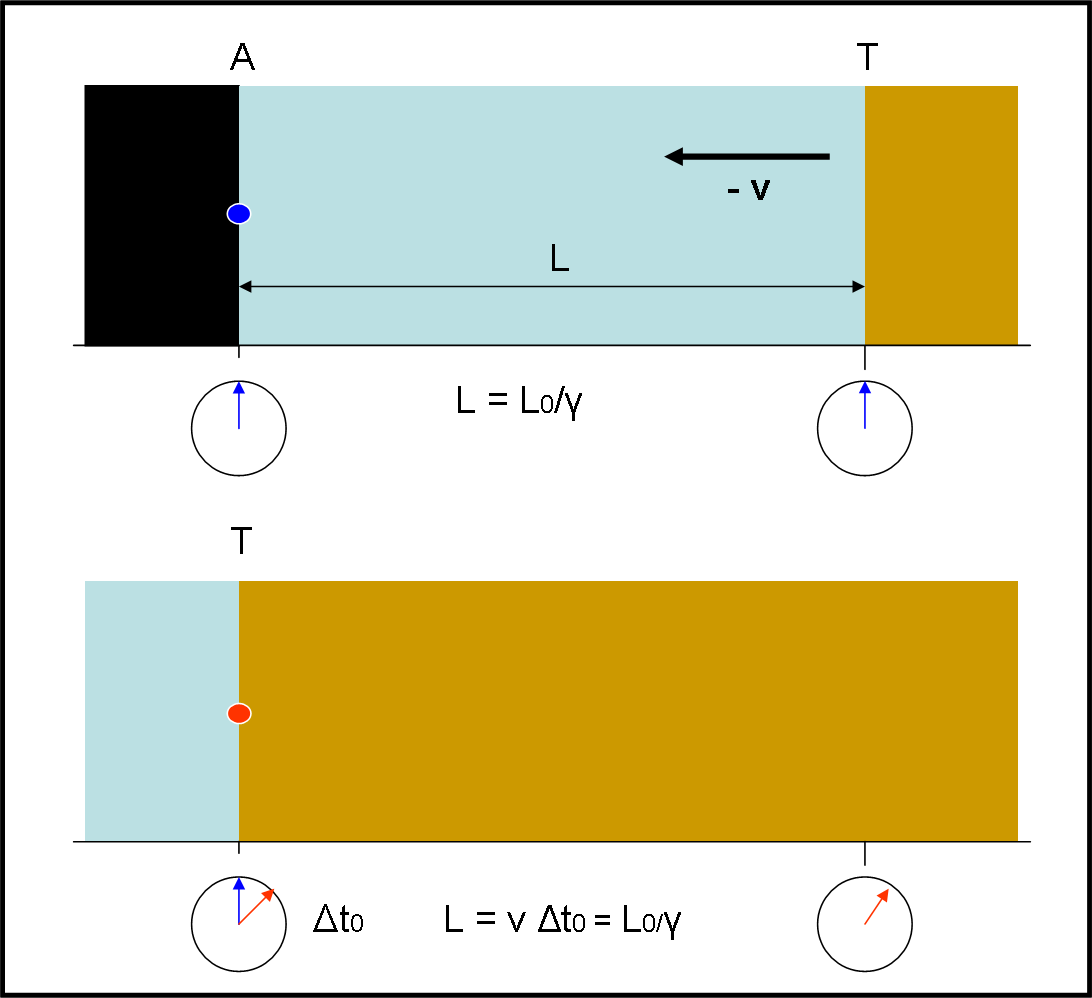
Dopo aver dilatato i tempi, divertiamoci, adesso, a contrarre le lunghezze, sempre per via puramente grafica. La dimostrazione è leggermente più complicata di quella precedente (ma tutto si basa sempre sulla necessità di usare più orologi). Come vedremo bisogna passare, prima, attraverso il tempo per arrivare, infine, alle lunghezze. Inoltre, solo la curva di calibrazione ci permetterà di capire che il nostro occhio, abituato alla geometria euclidea, può facilmente sbagliare…
Con quanto descritto finora, molti di voi sono già sicuramente in grado di determinare graficamente le due più famose ripercussioni della RR: la dilatazione dei tempi e la contrazione delle lunghezze. Senza alcuna formula, però… solo con una matita!
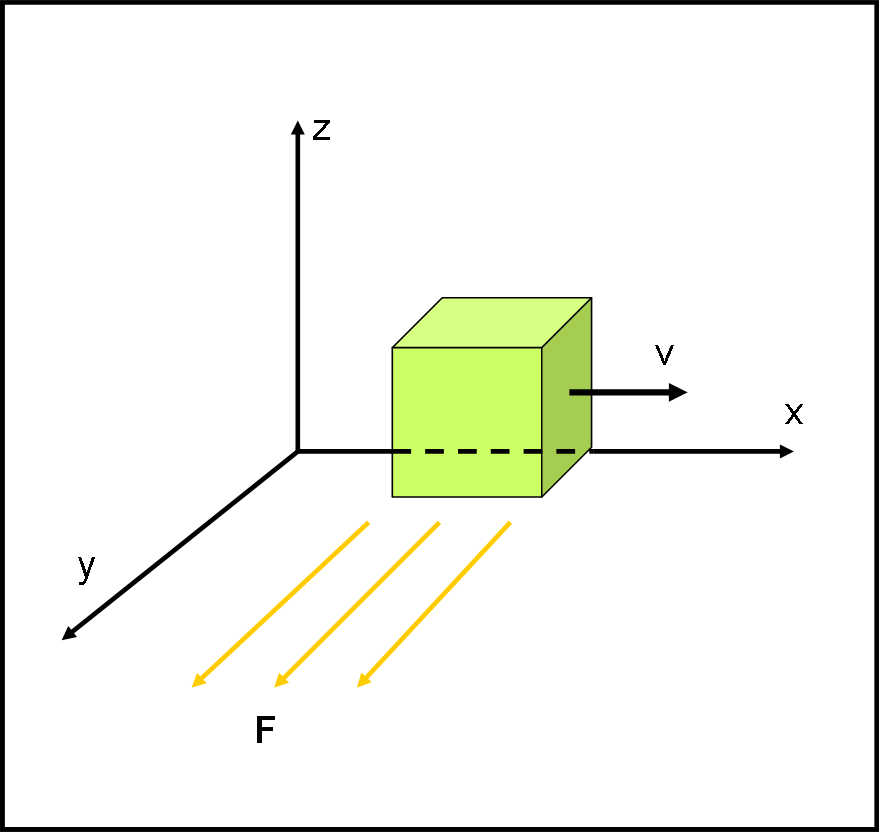
Questo quiz è decisamente difficile, ma qualcuno potrebbe aver voglia di provare (non vi sono formule complicate da applicare se non quelle che già conosciamo bene dalla relatività speciale).
Prima di proseguire con la composizione delle velocità in ambiente relativistico, fermiamoci un attimo a raccontare una favola un po’ triste che raccontano su Papalla. I personaggi principali sono i muoni, piccole particelle subatomiche. Sulla Terra, la favola è diventata realtà.
Con questo articolo di carattere "pratico" possiamo dire di avere concluso la base della relatività speciale o ristretta. Vi sono adesso due strade da seguire. Una ci porta alla sua rappresentazione nel celebre diagramma di Minkowski, l'altra alle conseguenze della nuova teoria sulle varie grandezze fisiche, nonché alla celeberrima formula che lega energia e massa. Devo ancora decidere quale delle due imboccare per prima. Tuttavia, per permettere di fare un ripasso più accurato della fase iniziale. e più fondamentale, ho pensato di riunire tutti gli articolo in uno solo e inserirlo prima in evidenza e poi negli approfondimenti. Lo chiameremo "Le basi della RR". Chi non ha seguito i primi quattordici capitoli avrà tempo di rivederseli con calma e in modo consecutivo; nel frattempo io cercherò di organizzare a andare avanti con la seconda parte.