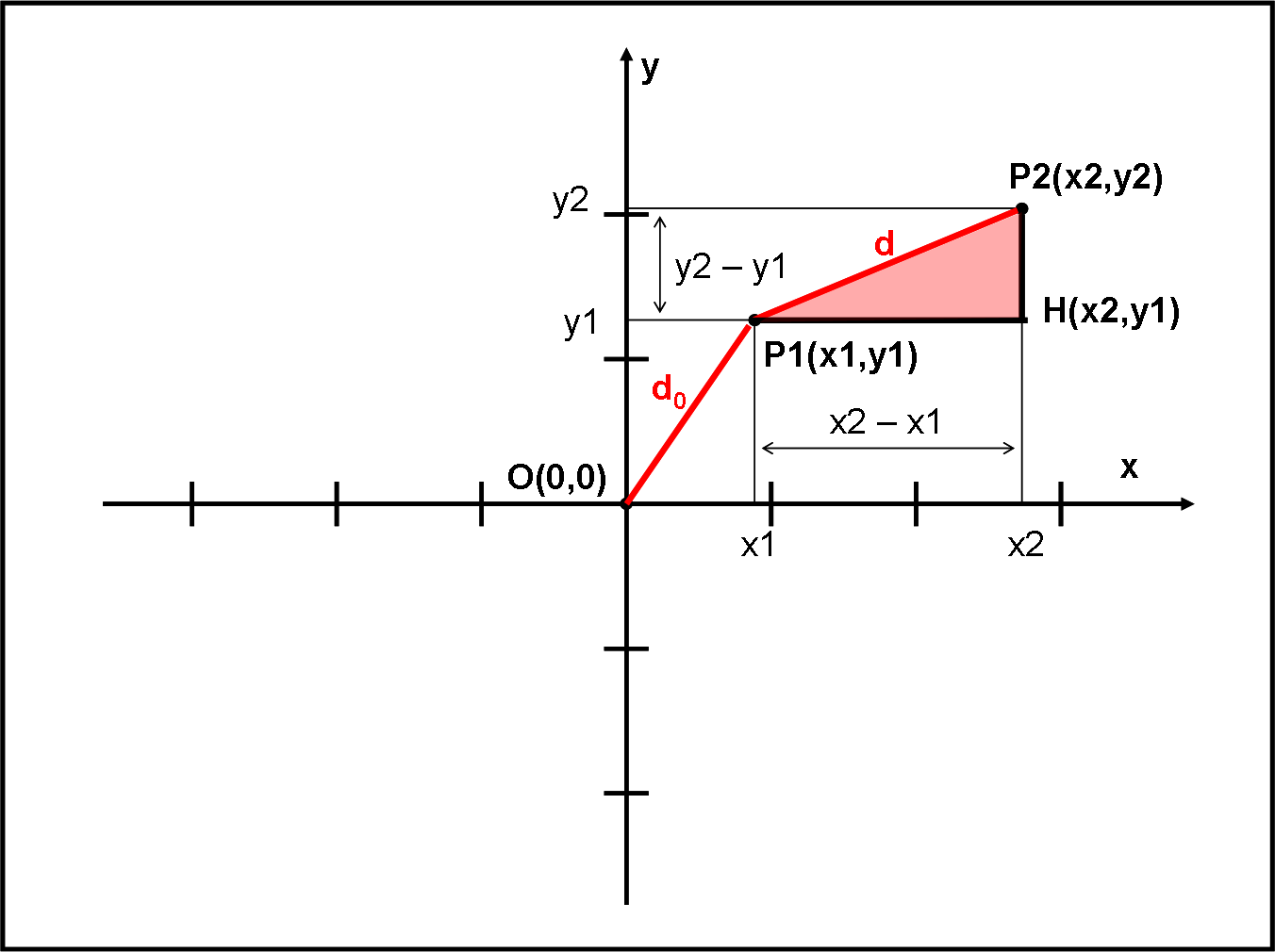
In questo articolo propongo alcuni degli argomenti affrontati da Enzo nel 6° articolo della serie “La relatività Generale al microscopio” applicati al caso particolare delle coordinate cartesiane e coordinate polari nello spazio Euclideo. L'obiettivo è di illustrare tramite queste due coordinate il percorso che porta al tensore metrico o metrica.
Ci siamo costruiti un sistema di riferimento semplice e utilissimo. Vedremo subito come utilizzarlo. Prima inseriremo nuove stazioni un po’ dappertutto e, chiamandole con le loro coordinate, sapremo trovarle immediatamente. Poi inizieremo a costruire monorotaie sempre più complicate. La matematica diventerà l’unico linguaggio in grado di aiutarci nella loro “sistemazione” nella rete ferroviaria, ossia nel piano del foglio.
Dopo esserci lanciati nelle strane piroette compiute da zero e infinito nel cercare di eseguire, tra di loro, le operazioni aritmetiche di base ed esserci accorti che non sempre tutto risulta banale e scontato (anzi…), facciamo un grande passo indietro. Abbiamo imparato a conoscere questi due concetti e/o punti e/o numeri così particolari. Ora possiamo cominciare proprio dall’inizio. Per far ciò costruiamo una rete ferroviaria di riferimento. E ci vorrà molto prima di lasciarla… I primi articoli di questo tipo saranno fin troppo banali per chi ha studiato analisi matematica. Vi prego di avere pazienza… e poi c’è sempre qualcosa da imparare, quando si parla di geometria e di matematica.