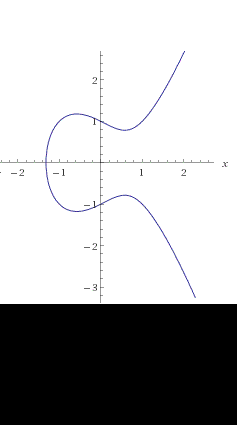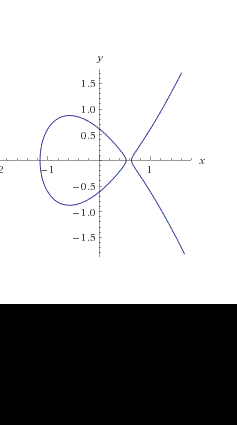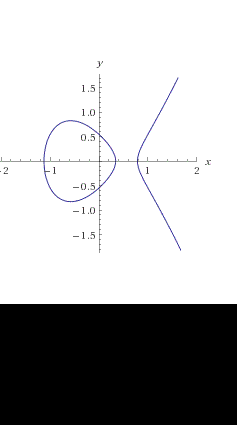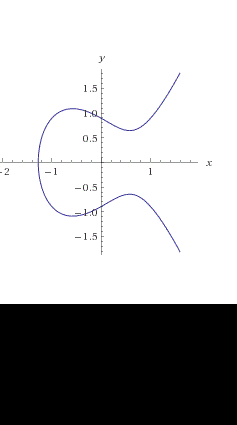
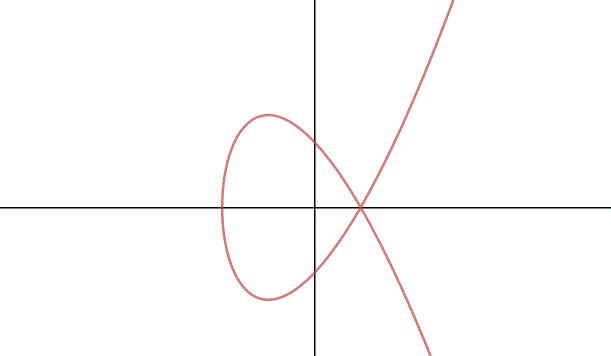
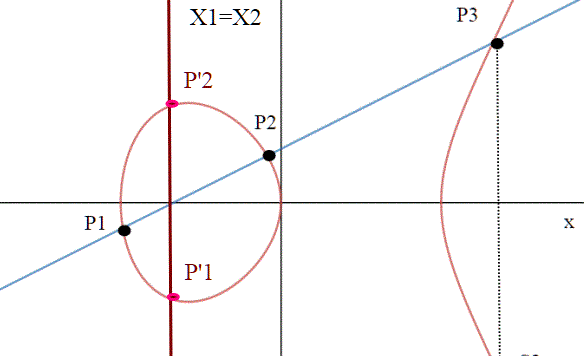Un riassunto su tutto quello che abbiamo visto sulle curve ellittiche,quiz compresi, che ci porta a concludere che esse costituiscono un gruppo con una particolare operazione interna. Questo fatto è fondamentale per l'impiego delle curve ellittiche in crittografia.
Il Mont-Saint-Michel ha le più alte maree sizigiali dell'Europa Continentale, è uno spettacolo indimenticabile!
Con la bassa marea il mare è a 15 km dalla costa. La marea arriva alla velocità di un cavallo al galoppo, con il livello del mare in aumento di 15 metri tra bassa e alta marea...
Indice di tutti gli articoli di Umberto presenti in archivio-Matematica Riprendiamo il discorso sulle curve ellittiche; nell' articolo precedente (qui), abbiamo trovato il punto all'infinito di una curva ellittica di equazione generica: ; esso coincide con il punto all'infinito dell'asse delle y; questo ci fa capire che la curva all'infinito è tangente all'asse delle y. […]
Se vogliamo parlare in modo totalmente corretto di equazioni ellittiche e di gruppi ellittici dobbiamo farlo all'interno del piano proiettivo. E' necessario introdurre il concetto di punto improprio o punto all'infinito, con una trattazione non strettamente formale, ma più che altro intuitiva.
Ho voluto fare un esempio di applicazione dei gruppi ciclici e dei campi su Zp (interi modulo p) per far capire che anche questa matematica un po' strana ha una applicazione fondamentale nella gestione della sicurezza delle informazioni. Senza saperlo, ogni volta che usiamo la carta di credito, usiamo anche i gruppi algebrici.
Per analizzare correttamente le equazioni algebriche sotto nuovi punti di vista (tipo quelle ellittiche usate da Wiles per la dimostrazione della congettura di Fermat) bisogna avere a disposizione una nuova struttura algebrica: il Campo. Nell'immagine Euclide; i suoi algoritmi sono ancora attuali perfino nelle moderne congetture matematiche.