Una breve aggiunta relativa alle funzioni iperboliche e alle loro funzioni inverse.
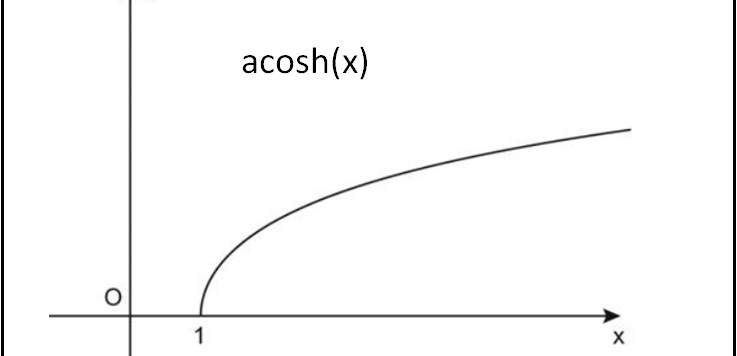

Non ne abbiamo mai parlato, ma questo metodo di integrazione permette di risolvere molti problemi collegati alla soluzioni di integrali che sembrano apparentemente molto difficili, se non impossibili. Ci permette, soprattutto, di proporre quiz piuttosto interessanti e utili.
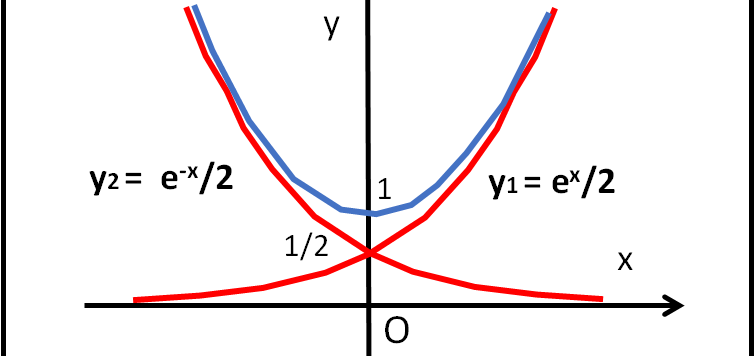
Verifichiamo ancora una volta il significato delle funzioni iperboliche e vediamo che forma hanno. In fondo, è proprio questa forma che ci verrà utile in seguito, anche per comprendere le argomentazioni di Galileo Galilei.
Come detto, questa serie di articoli vuole essere veramente divulgativa e adatta a qualsiasi livello, sempre che si abbia già un'infarinatura dei concetti di limite, derivata e integrale. Per ottenere ciò, penso che non mi picchierete se a volte sarò ripetitivo e quasi banale. Nella versione definitiva, si potrà sempre cercare di compattare meglio la materia e renderla più uniforme. Per adesso pensiamo ad affrontare nel modo più chiaro possibile i concetti fondamentali.

Non bastava l'accelerazione a complicare la vita! Adesso arriva anche il jerk e si tira dietro tutti i suoi parenti.
E va bene, via, riprendiamo il discorso e vediamo che altro ci aspetta!
Le derivate comportano sicuramente dei problemi quando le funzioni sono piuttosto complesse. Tuttavia, con un po’ di attenzione e di pazienza, si riesce a portare a compimento l’esercizio. Insomma, le derivate spaventano, ma non poi tanto. Dovrebbe succedere lo stesso con gli integrali che sono l’operazione inversa. E, invece, come tutte le operazioni inverse, le difficoltà crescono di molto. Non è, quindi, assurdo giudicare gli integrali ben più ostici delle derivate. Capita a tutti, anche ai migliori matematici…
Eccovi la soluzione che io ho considerato come la più semplice e immediata. Non ve ne era nemmeno bisogno, a seguito delle risposte mandatemi. Tuttavia, ripetere fa sempre bene...
Vi chiedo perdono per due motivi. Innanzitutto, perché il problema fisico (ma anche matematico) è di estrema semplicità. Inoltre, perché ho scritto un articolo di risposta assurdamente lungo per ciò che si chiedeva. Spero, però, che serva a fare un bel ripasso di derivate e limiti…
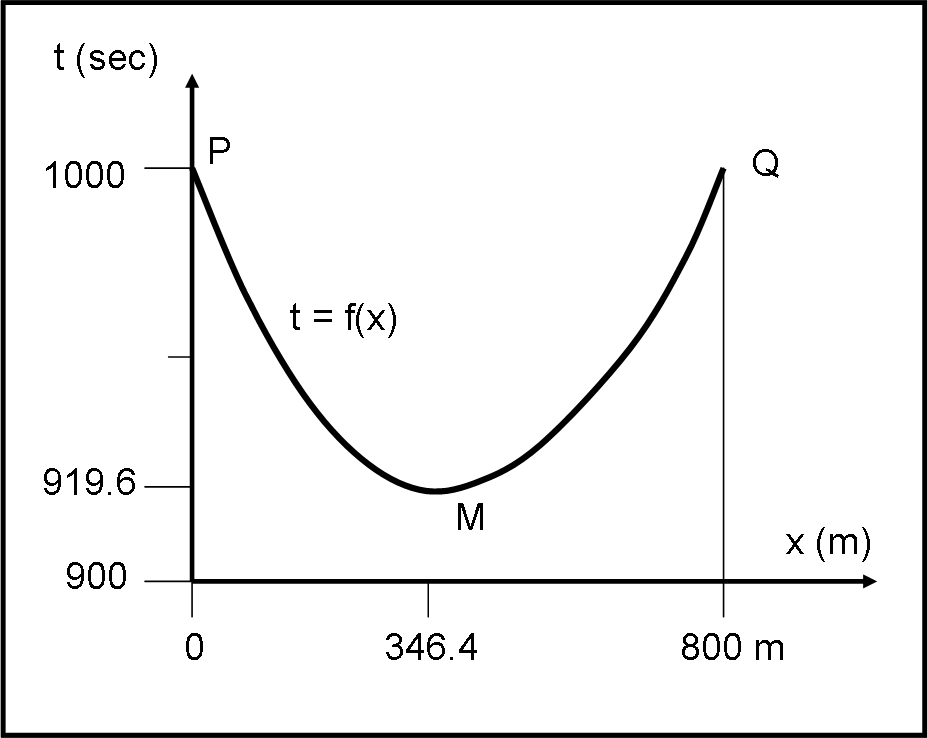
Approfittiamo della soluzione al quiz sul "naufrago" per fare un piccolo ripasso di derivate e di studio di funzione. Un caso veramente elementare... credetemi!
Questo articolo risponde al quiz sul buco della Terra. Ma, in realtà, va ben oltre e ci insegna a valutare sempre meglio la semplice genialità di Newton oltre che darci uno spunto per capire, ancora una volta, cosa s’intende per curvatura spaziotemporale. Questo è il bello della fisica: ogni argomento riesce a collegarsi strettamente a un altro e poco importa se siamo vicini alla Terra o in prossimità di un buco nero. Devo complimentarmi con alcuni di voi (non faccio nomi) che hanno quasi completamente risolto il problema e che, quando ci si sono avvicinati soltanto, hanno mostrato di aver compreso appieno il concetto di fondo su cui lavorare. Le leggi della fisica e la loro eleganza e generalità si imparano un po’ alla volta. Siamo tutti studenti che cerchiamo di aggiungere continuamente un mattoncino alla nostra costruzione, che, se ha le basi solide, non rischierà più di cadere.
In questo file ho inserito tutti gli articoli riguardanti la matematica, dalla conoscenza delle zero e dell'infinito fino alle derivate e allo studio di funzioni. Il linguaggio è quello più semplice e adatto a tutti... Come dice il nostro Paolo: Non serve descriverne i tratti somatici, fissandoli nella propria memoria, la matematica ha bisogno di essere compresa per mostrare la sua semplicità, solo così il brutto carattere lascia il posto al sorriso.
Cari amici, non sono molto contento dei risultati (lo dico perché siamo tra AMICI, ovviamente). Innanzitutto, perché solo pochissimi hanno risposto. Ma soprattutto non mi è piaciuto il modo come hanno risposto. Perché? Quasi tutti non hanno seguito il semplice procedimento che avevo illustrato nel capitolo 24, ma hanno liberamente utilizzato concetti e procedimenti che ancora non avevo spiegato. Tutto ciò può dimostrare che loro sono bravi e preparati, ma ha creato molta confusione nei meno preparati. Probabilmente aiutandoli a lasciar perdere un argomento che si stava complicando in modo non gestibile attraverso le lezioni già pubblicate. Insomma, siamo caduti nel solito errore che fa odiare la matematica: la perdita di un ordine semplice, chiaro e umile. Il succo delle 24 lezioni non è, invece, questo e nemmeno quello di fare classifiche di bravura, ma solo quello di tentare di fare amare una materia fondamentale per capire l’Universo.
Attraverso il capitolo 24 siamo ormai in grado di calcolare i punti particolari di funzioni abbastanza semplici. Scopriremo che esistono anche altri punti peculiari e altri metodi di calcolo, ma per adesso accontentiamoci di quanto descritto finora. Forza, le vacanze sono finite e si torna al lavoro! Un piccolo test prima di andare avanti. Se non riuscite… ditelo senza vergogna (magari in privato), in modo che possa intervenire subito. Sarebbe assurdo continuare se sono sorti dei problemi già adesso.
Un breve articolo, dove spiego in modo più dettagliato come si risolvono le derivate che vi avevo dato come esercizio. Se rimangono problemi, fatemelo presente. Tra non molto partiremo con lo studio di funzione… finalmente!
Eccovi i risultati degli esercizi sulle derivate. Controllate, riprovate, meditate e... chiedete, ovviamente!!!