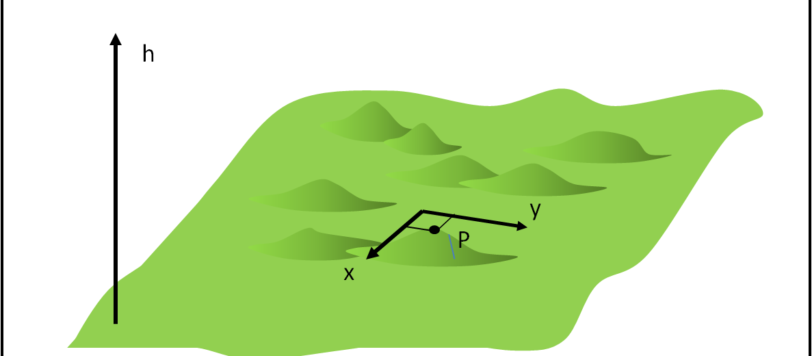
E' venuta l'ora di entrare in un campo e. dato che è molto irregolare, vogliamo associare a ogni suo punto lo scostamento rispetto a un livello costante. In altre parole, associare a ogni punto il valore del campo. Lo facciamo a piccoli passi spostandoci di poco in ogni direzione. Alla fine otteniamo una "mappatura" tridimensionale perfetta. Ci accorgiamo che anche l'aggettivo "tridimensionale" perde di significato...
Seguendo gli articoli di Enzo ho notato che citava l'utilizzo della "lagrangiana", per la soluzione di un problema relativo ai punti lagrangiani. Avevo già visto citato questo misterioso oggetto anche da altri che ne parlavano come di una cosa fondamentale nella fisica classica e, ancora di più, nella fisica moderna. A grandi linee sapevo di cosa si trattasse, ma non avevo mai approfondito l'argomento. La citazione di Enzo mi ha incuriosito ulteriormente e ho cercato di capire meglio cosa fosse questa lagrangiana. Questo articolo raccoglie tutti i capitoli usciti a puntate ed è stato inserito negli approfondimenti.
Il viaggio verso l'equazione di Eulero-Lagrange continua.
Occorre fare ancora una tappa per completare la conoscenza delle derivate utilizzate nella equazione.
Come nei gruppi ben affiatati che affrontano i sentieri di montagna, procediamo ad un passo che spero possa permettere a tutti di godere del percorso.