E perché no ? Ecco a voi una bella fake news relativistica...

Misurata la dilatazione dei tempi, dovuta alla curvatura dello spaziotempo, su scala millimetrica.

Tutti sanno come lavora il GPS? Beh.., penso proprio di sì dato che viene usato molto più delle bussole di una volta. Ma tutti sanno anche che se la RR e la RG non fossero tenute in conto l’apparecchiatura non potrebbe funzionare? Cercheremo di dimostrarlo con un esempio molto istruttivo che richiamerà (non fa mai male) il mix tra RR e RG che esiste e va tenuto in conto anche quando qualcosa si muove in un campo gravitazionale relativamente debole come quello della Terra.
Avrete capito subito che il quiz è stato predisposto per fare (una volta per tutte) chiarezza sul paradosso dei gemelli. Ragione per cui, risolviamo il problema in vari modi, accorgendoci che, alla fine, si usa sempre lo stesso concetto, quello del cambiamento di sistema di riferimento inerziale.
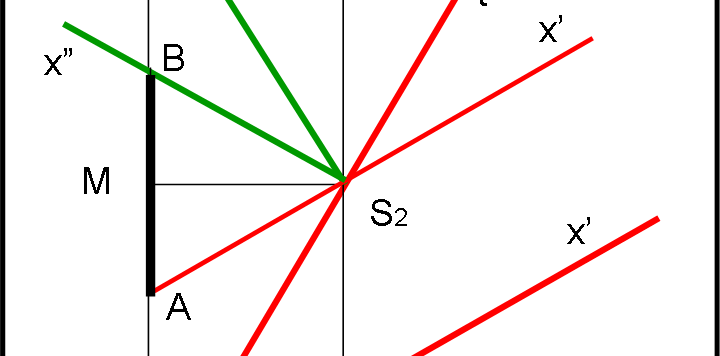
Se la Relatività Ristretta (RR) permette di descrivere l'Universo e le leggi fisiche dei sistemi inerziali attraverso poche formule fondamentali basate su un numero ristretto di postulati, lo spaziotempo di Minkowski e il corrispondente diagramma ce ne regalano una visione grafica di grande generalità. Tutto l'Universo soggetto alla RR può essere rappresentato in un foglio di carta, utilizzando due sole coordinate. Il diagramma di Minkowski permette di comprendere appieno e di visualizzare direttamente la RR. Le sue applicazioni sono enormi e si estendono anche alla Relatività Generale.
Dopo aver divagato un poco con il paradosso dei gemelli, torniamo al nostro diagramma di Minkowski e iniziamo a vedere come sia facile ottenere graficamente la dilatazione dei tempi e la contrazione delle lunghezze. Ricordate che è fondamentale aver compreso bene il concetto di relatività della simultaneità e poco altro. Iniziamo con la parte più semplice, quella che riguarda la dilatazione dei tempi.
Questa è la prima parte della Teoria della Relatività Ristretta o Speciale. Si parte dalla relatività galileiana e si arriva agli effetti che derivano dai postulati di Einstein: dilatazione dei tempi e contrazione delle lunghezze. Facciamo conoscenza con la trasformazione di Lorentz , il passo fondamentale per passare da spazio e tempo a spaziotempo. Ricordiamo che l'intera teoria si riferisce SOLO a sistemi di riferimento in moto rettilineo uniforme tra loro. Non sono quindi valutate le deformazioni spaziotemporali causate dalla gravità e dalla sua accelerazione. La relatività ristretta è quindi una teoria perfettamente simmetrica e niente ha a che vedere con le deformazioni univoche causate dalla relatività generale. Negli articoli seguenti, si toccheranno le ripercussioni della relatività ristretta sulle varie grandezze fisiche (tra cui la celebre E = mc2) e la sua rappresentazione nel diagramma spaziotemporale di Minkowski.

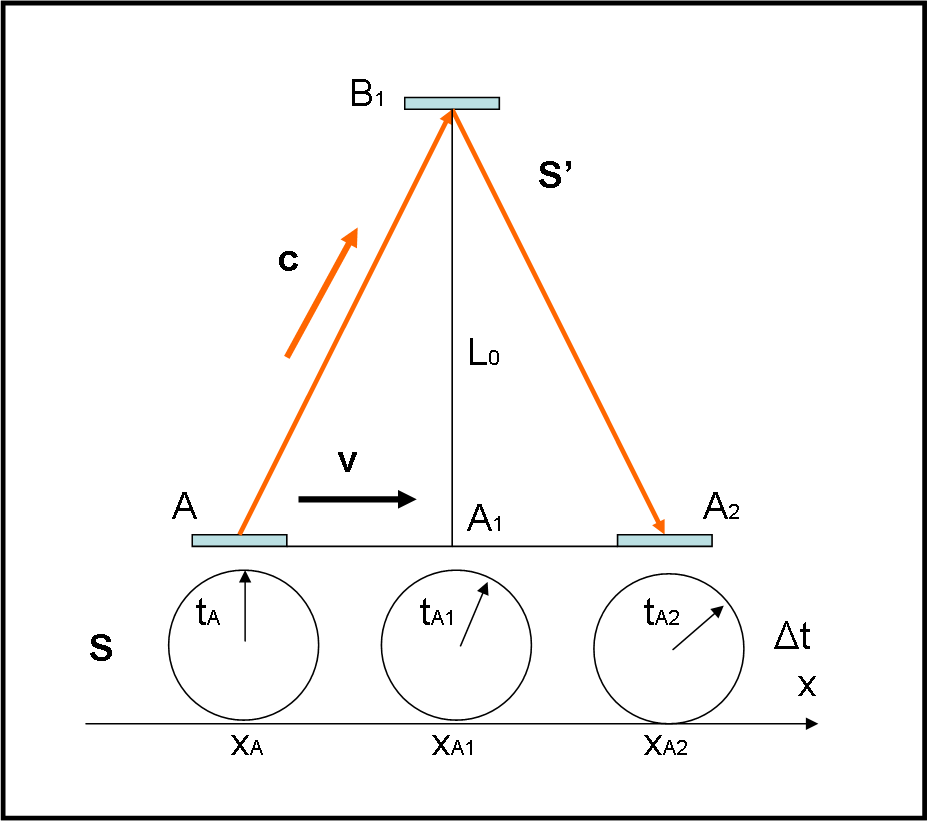
Ritroviamo la trasformazione di Lorentz attraverso uno “strano” orologio, il cui tic-tac è rapidissimo: l’orologio di luce. Basta un triangolo rettangolo e il gioco è fatto. Ci occupiamo, per adesso, solo della “dilatazione” dei tempi. Introduciamo anche, molto superficialmente, la distanza invariante dello spaziotempo di Minkowski. Ci servirà in seguito…e come!