Abbiamo deciso di cambiare la definizione di quantità di moto. Dirlo è una bella cosa, ma farlo è un’altra. La soluzione migliore sembrerebbe quella di considerare la massa come una funzione della velocità. Non abbiamo certo detto una cosa da poco. Basterebbe pensare che ciò vorrebbe dire che l’inerzia di un corpo cambia al variare della sua velocità. Teoricamente potrebbe diventare infinita. Non ci resta che fare questo tentativo e controllare, con molta attenzione, se questa sconvolgente ipotesi riesce, veramente, a conservare la nuova quantità di moto. Questo articolo è il più “duro”, ma niente di veramente difficile.
Questo articolo è molto corto. Preferiamo mangiare la “torta” a piccoli tranci per permetterci di gustarla fino in fondo. Dimostrare che la quantità di moto “classica” non si conserva nella Relatività Ristretta è un punto di arrivo fondamentale e va compreso perfettamente bene. Una conclusione, in realtà, banale, ma che ci obbliga a modificare tutta la dinamica conosciuta fino ad allora. Ricordiamo, comunque, che stiamo parlando di velocità comparabili a quella della luce. Se giocassimo a palline con un nostro amico che va in bicicletta niente cambierebbe rispetto alle descrizioni di Galileo.
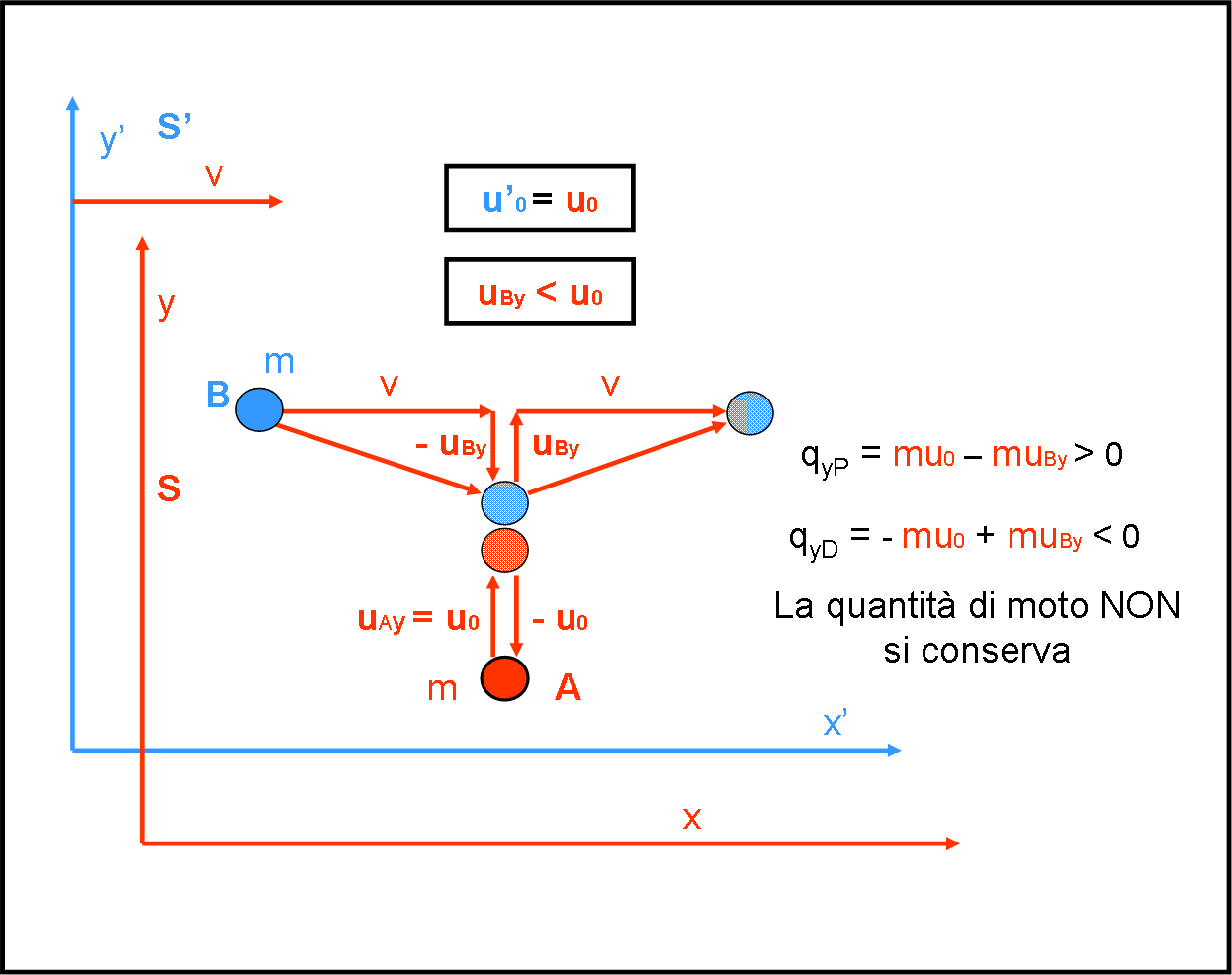
In questo secondo articolo costruiamo un esperimento relativo all'urto elastico di due palline, appartenenti a due sistemi diversi. Prima manteniamo fermi i due sistemi e dopo facciamo muovere il primo, rimanendo in ambito galileiano. Cosa succede alla quantità di moto delle due palline?
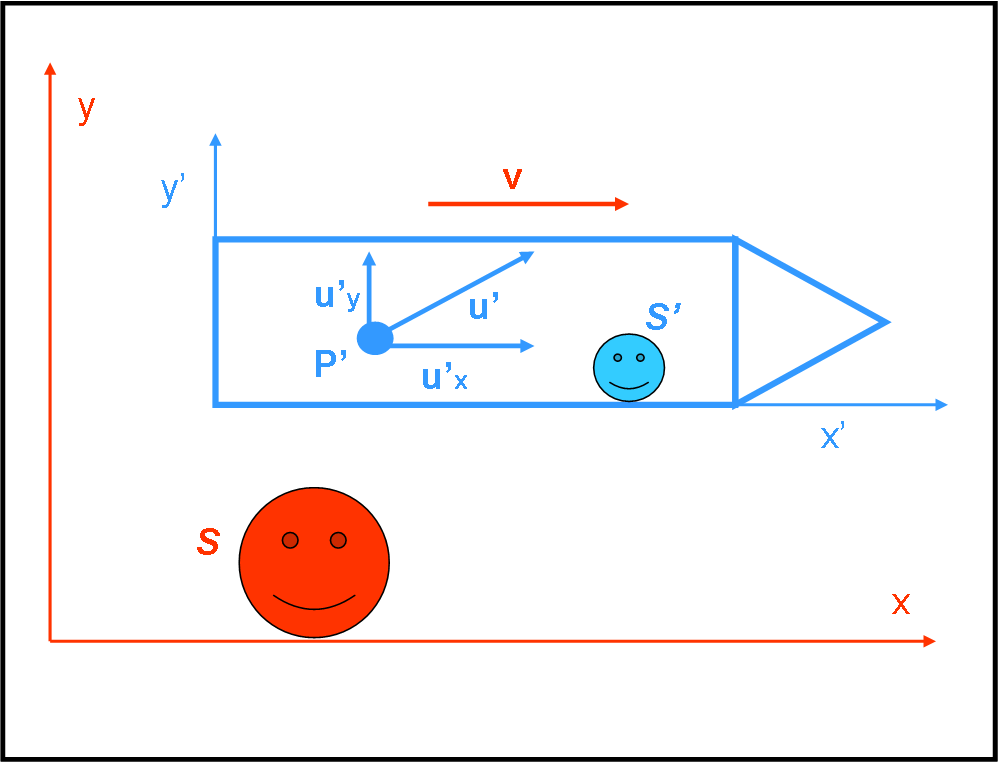
Siamo pronti per partire con la dinamica relativistica. Per far ciò è fondamentale descrivere, prima di tutto, come la quantità di moto sia costretta a cambiare per potersi conservare. Normalmente questa parte si dà per assodata o si spiega -spesso- in modo poco chiaro, incentrando tutto sulla massa relativistica, gioia e dolore dal punto di vista concettuale. Ho cercato di raggiungere lo scopo nel modo più semplice possibile, evitando, però, semplificazioni che avrebbero generato eventuali confusioni. Ho deciso di pubblicare questa parte iniziale della dinamica relativistica (DR) prima della fine degli integrali, in quanto non ne ha bisogno. Vi prego sinceramente di esporre tutti i dubbi senza paura. Ricordiamoci che senza questa base di partenza i nodi verrebbero, comunque, al pettine più tardi… Fatemi anche capire (in tanti) se … avete capito! Basta un OK...
Cari amici, vi state -forse- accorgendo che ho ridotto il numero di articoli... In realtà, ho qualche problema logistico in casa, ma la vera ragione non è quella. Diciamoci le cose con chiarezza e onestà: "Sto diventando matto con l'inizio della dinamica relativistica!". Per essere più chiaro, i problemi sorgono con la definizione della NUOVA […]
Eccovi la soluzione che io ho considerato come la più semplice e immediata. Non ve ne era nemmeno bisogno, a seguito delle risposte mandatemi. Tuttavia, ripetere fa sempre bene...
Il nostro caro e appassionato amico Umberto freme dalla voglia di scatenarsi nella dinamica relativistica. Lo ammiro, lo capisco benissimo e penso anche che non sia il solo. Posso assicurarvi che sto già preparando le lezioni corrispondenti, facendo opera non facile di sintesi e di selezione. Penso che, alla fine, saranno contenti tutti, sia i meno preparati che i più smaliziati. Tuttavia, non voglio farmi convincere ad accelerare i tempi. Vorrei dare il meglio di me, senza fretta, ma anche completare il bagaglio culturale necessario per affrontare la parte più esaltante della RR con la dovuta preparazione di base. Eccovi, quindi, un piccolo antipasto, che non dice niente di significativo, ma che cerca di inquadrare la problematica sotto vari punti di vista e che, spero, faccia digerire meglio gli integrali.
- 1
- 2

