Torniamo a parlare di quel genio matematico che è stato Srinivasa Aiyangar Ramanujan, l'uomo che giocava con la matematica e che non aveva paura dell'infinito.
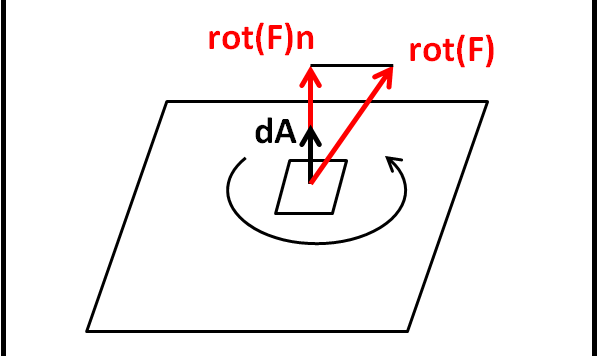
Descriviamo i due teoremi fondamentali (della divergenza e del rotore) che ci permetteranno di passare dalle equazioni di Maxwell in forma integrale a quelle in forma differenziale.
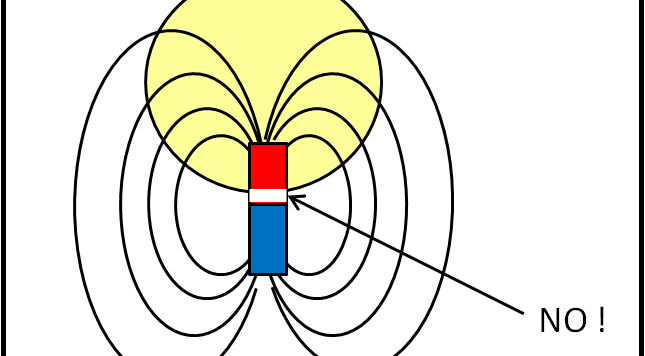
Un capitolo veramente corto e zeppo di concetti già detti e ridetti. Ma mi è sembrato giusto dare a ogni equazione la sua visibilità...
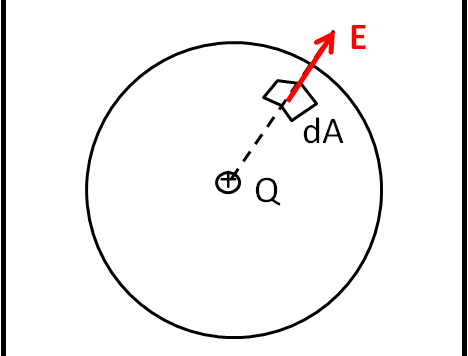
Cominciamo da capo, cercando di scrivere con un linguaggio matematico (semplice) le varie equazioni. Scusate le ripetizioni, ma è meglio battere il chiodo due volte e anche più. Come già detto non spaventatevi dei segni di integrazione o di derivata e pensateli come somme e differenze lungo una certa direzione.
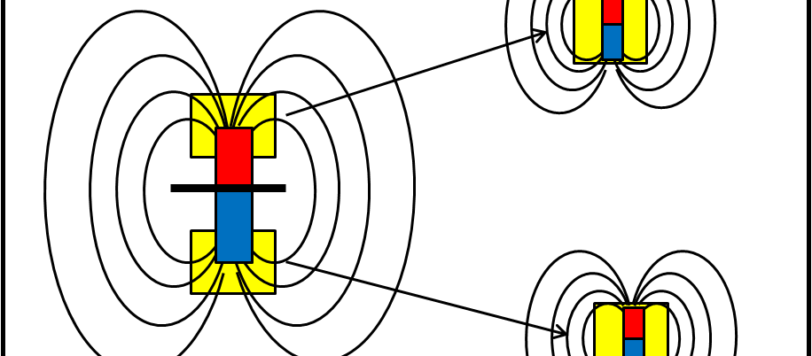
Avviciniamoci a grandi linee e in modo ancora piuttosto qualitativo alle prime due equazioni di Maxwell. Un piccolo antipasto per avere un'idea dei concetti di base. I due fratelli gemelli (campo elettrico e campo magnetico) entrano prepotentemente in scena!
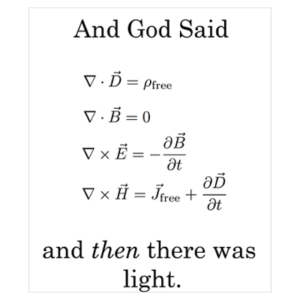
Forza e coraggio... iniziamo il nostro cammino verso le equazioni di Maxwell prima, e verso il campo elettromagnetico poi. Un percorso abbastanza lungo, ma che è stato fondamentale sia per le applicazioni tecniche e pratiche, che dominano il mondo attuale, sia per la formulazione della relatività di Einstein. L'intera trattazione può ancora essere modificata qualora creasse difficoltà superabili. Vi invito, perciò, ad aiutarmi nelle eventuali migliorie. L'argomento è troppo importante per non cercare di renderlo il più comprensibile possibile. Buon viaggio!