Basta osservare attentamente un trapezio e tutto diventa banale...
Un quiz che vi permette di sfidare lo stesso Euclide, privandolo del compasso.
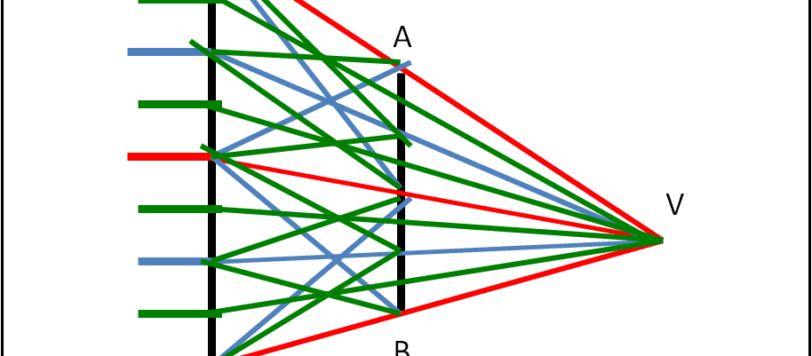
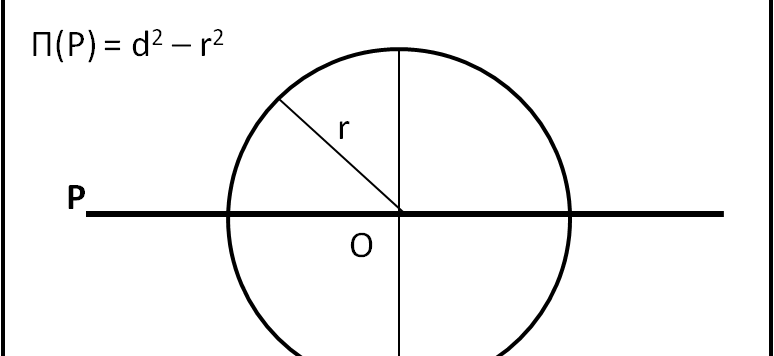
Il più grande geometra di tutti i tempi dimostra che anche i punti hanno una loro "potenza".
Una dimostrazione quasi magica di Euclide dimostra l'infinità dei numeri primi. E ancora non si conosceva l'algebra....
Mi sono accorto che li abbiamo spesso usati, ma non ne abbiamo mai fatto una vera storia. Eppure rimangono uno dei problemi insoluti nella matematica. Sto parlando dei numeri primi e della loro "solitudine" che non mi trova d'accordo col pensiero di Odifreddi.
Ancora sulla sezione aurea, ma mettendo in luce un'altra piccola dimenticanza di Euclide & Co.
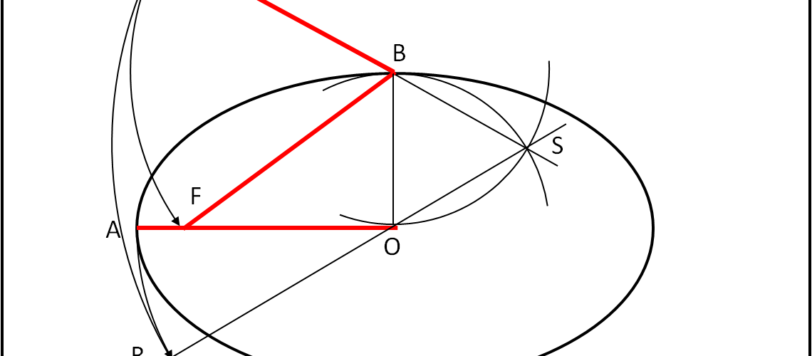
Mi spiace che nessuno abbia provato a risolvere questo "problema" che ci riporta alla Scuola d'Atene. Io trovo queste antiche costruzioni veramente interessanti e istruttive. Riporto, perciò, tutti i passaggi.
Questo articolo non è un quiz, ma una richiesta di collaborazione nel pieno spirito del nostro Circolo. L'argomento è ancora quello delle costruzioni geometriche dei greci ed in particolare della Scuola di Atene.
La soluzione è probabilmente più facile di quello che poteva sembrare a prima vista. Maurizio è riuscito ad arrivare al dunque (dovrebbe passare un mesetto a casa dei pappidi che ama veramente tanto). Tuttavia, io presento un’altra soluzione (ben poco diversa) che fa uso di un teorema di Euclide tra quelli meno noti…
Diamo QUATTRO soluzioni per il quiz geometrico sullo strano quadrilatero confinante con il terreno di Nobody. Se ne arrivassero di nuove le aggiungeremo. Per cui guardate bene il “quattro” iniziale, se diventasse cinque o sei sapreste che c’è qualcosa di nuovo da leggere…
Euclide non scherzava come maestro di geometria, ma sembra che scherzasse con i suoi quiz matematici... Se lo faceva lui, possiamo farlo anche noi...
Non considerate noioso questo articolo. Da un lato abbiamo a che fare con problemi di geometria apparentemente più che banali, ma, dall'altra, entriamo prepotentemente nella Scuola di Atene, dove dire "geometria" è un modo di vivere e di pensare. Seguendo poche regole prefissate, siamo in grado di ottenere ciò che l'algebra e la geometria analitica ritroveranno dopo secoli. Un viaggio entusiasmante e -soprattutto- molto divertente.
Abbiamo visto numeri difettivi e numeri eccedenti, ciascuno con i suoi problemi esistenziali. I loro stessi nomi indicano chiaramente che devono esistere anche dei numeri perfetti, ossia tali che la somma dei loro divisori sia esattamente uguale al numero. E si apre un argomento ancora oggi non risolto del tutto…
Per parlare dei numeri, non basterebbero tutti i libri esistenti al mondo. Essi non sono solo le lettere della matematica, ma molto, molto di più. La matematica (costruita da noi) usa i numeri, ma solitamente non s’interessa di cosa essi siano realmente e di come possano essere veramente descritti. Per capire meglio il loro mondo fantastico è necessario tornare all’antica Grecia (forse anche prima, ma i dati in nostro possesso sono troppo scarsi), in particolare alla scuola di Pitagora. Scopriremo un vero universo, pur limitandoci a poche nozioni. Scopriremo anche che la nostra tecnologia non è ancora riuscita a risolvere molti dei loro segreti.
Questo è solo un preambolo estremamente riduttivo e rozzo (addirittura non del tutto esatto). Serve solo per farsi la bocca in attesa di quanto promesso a Dany e ad Alvy. Tutto gira intorno al quinto postulato di Euclide, quello delle rette parallele. Ma per discuterne a fondo e per applicarlo alla fisica dell’Universo è necessario fare un lungo percorso storico e matematico. Fin dall’inizio, però, capirete bene perché il nostro “circolo” (e il libro precedente) si chiama Infinito TEATRO del Cosmo.