Quando Feynman era studente universitario riusciva già a proporre problemi di non facile soluzione. Uno di questi gli costò, però, il divieto di entrare nel laboratorio dell'Istituto. La fece proprio grossa...
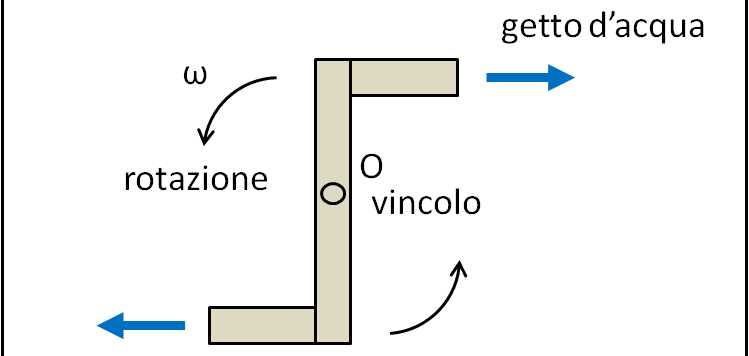

Quando Feynman era studente universitario riusciva già a proporre problemi di non facile soluzione. Uno di questi gli costò, però, il divieto di entrare nel laboratorio dell'Istituto. La fece proprio grossa...

Anche se poco conosciuto, esiste un metodo di derivazione di funzioni complicate ideato da Feynman. Pur non essendo molto vantaggioso, può aiutare in casi piuttosto intricati.

Questo articolo è già stato pubblicato e lo avevamo pensato come primo di una serie basata sulla libera traduzione di alcune delle celeberrime lezioni di fisica tenute da Richard Feynman alla Cornell University dal 1961 al 1964. Ma, nel momento in cui abbiamo provato a scrivere il seguito, ci siamo resi conto che il contributo originale alla comprensione della gravità si esaurisce in questa prima parte e andare avanti con una semplice opera di traduzione delle sue lezioni (peraltro già disponibile e facilmente acquistabile anche in rete), non ci sembra avere alcun valore aggiunto per i nostri lettori.
Riproponiamo, pertanto, questo articolo per riportarlo alla vostra attenzione e aggiungere una gocciolina all'oceano della divulgazione del Feynman-pensiero. Con l'occasione, lo inseriamo in quel vaso di Pandora che è l'archivio di questo Circolo-Blog, per la precisione nella sezione dedicata alla Dinamica e Meccanica in Fisica classica.

"Nessuna quantità di esperimenti potrà dimostrare che ho ragione; un unico esperimento potrà dimostrare che ho sbagliato" (Albert Einstein)

Inizia un progetto piuttosto ambizioso: la traduzione in modo molto libero -e ridotto- di alcune delle celeberrime lezioni sulla fisica base di Richard Feynman, tenute alla Cornell University dal 1961 al 1964. Un giusto ricordo di chi ha cercato, con tutto se stesso, di impartire interesse e capacità di ragionamento nei futuri uomini di pensiero. Tempo perso? Forse sì, ma mi basterebbe che anche un solo giovane trovasse spunto per cambiare la visione succube e passiva della propria esistenza.

Lo abbiamo già proposto altre volte in passato, ma è sempre un piacere (e un dovere!) mantenerne vivo il ricordo... quale occasione migliore della scellerata approvazione di una legge (per ora solo al Senato) che equipara l'agricoltura biodinamica, basata su superstizione ed esoterismo, a quella biologica?

La notizia è di quelle in grado di cambiare il destino dell'umanità: il Nobel per la Fisica Richard Feynman aveva brillantemente risolto il mistero di Babbo Natale! Se non lo ha reso noto subito, è solo perché riteneva che l'umanità non fosse ancora pronta a cambiare il proprio destino. Ma, per nostra fortuna, ha lasciato in eredità il prezioso segreto a Vin-Census che oggi ha deciso di farne dono solo a chi ha sufficiente fantasia e ingenuità per comprenderlo. Per gli altri questo articolo sarà invisibile, quindi, se lo state vedendo, è già buon segno...

Questo articolo riunisce le varie puntate relative alla lezione "persa" di Feynman, in cui riesce a ricavare le leggi di Keplero basandosi soltanto sulle leggi di Newton (è stato anche inserito nell'archivio sotto Meccanica Celeste). Il tutto senza nemmeno un'equazione differenziale, ma solo giocando su triangoli uguali e su un diagramma geniale. Una trattazione talmente elegante e semplice che deve essere patrimonio della conoscenza di chiunque abbia vera passione per la fisica.
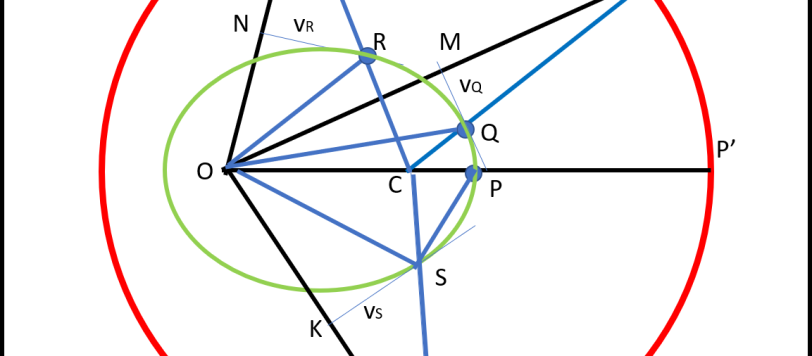
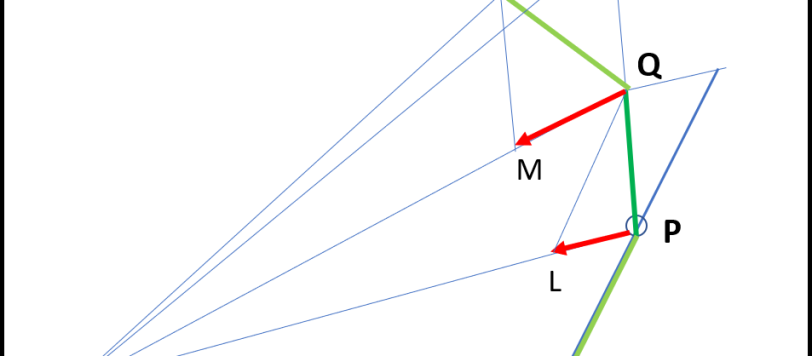
Nella puntata precedente eravamo riusciti a costruire il diagramma delle velocità basandoci sui primi due principi della dinamica e sulle prime due leggi di Keplero. Non ci resta che utilizzare questo geniale diagramma per dimostrare che la curva della traiettoria è proprio un'ellisse. Chi ha seguito i vari articoli si sarà già accorto che il diagramma delle velocità assomiglia in tutto e per tutto al cerchio iniziale della prima puntata. Basterebbe applicare a lui il procedimento usato allora e salterebbe fuori l'ellisse.
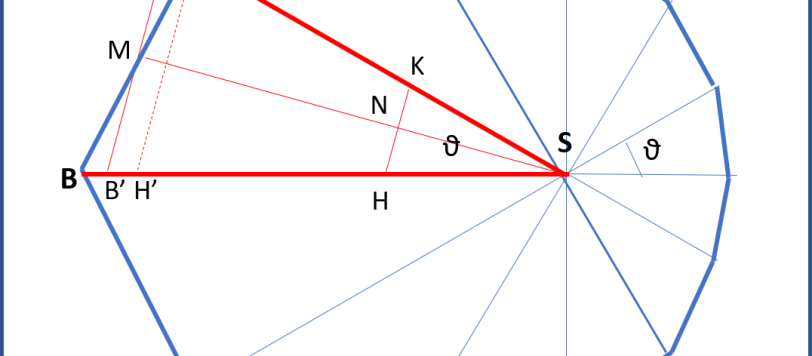
Abbiamo costruito il diagramma delle velocità corrispondente a una traiettoria che segua la seconda legge di Keplero e in cui la forza di attrazione vada con l'inverso della distanza al quadrato. Tuttavia, non sappiamo ancora che traiettoria sia e, soprattutto, non abbiamo ancora dimostrato che il diagramma delle velocità sia proprio un poligono regolare. Iniziamo con quest'ultimo problema.
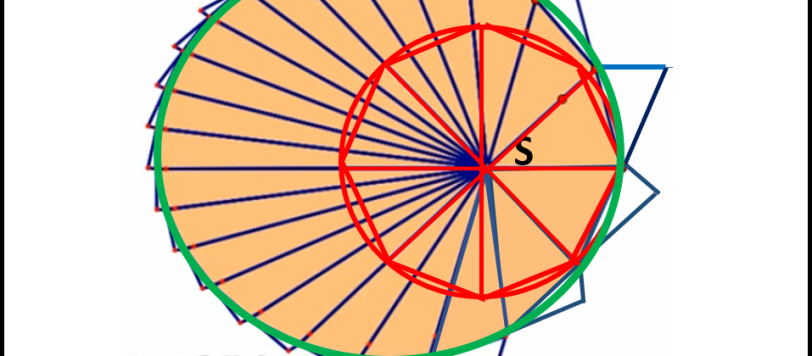
La volta scorsa eravamo rimasti "in panne" dato che, pur avendo ricavato la seconda legge di Keplero, ben poco si poteva dire sulla traiettoria di un pianeta attorno al Sole. Per fare questo passo in avanti è necessario conoscere come agisce la forza esercitata dal Sole, in funzione della distanza del pianeta. Ho aggiunto un asterisco solo perché bisogna capire molto bene la costruzione elementare di un nuovo diagramma...
Non stupitevi dell'unico asterisco inserito nel titolo. L'articolo, in realtà, non va oltre e ciò che è necessario sapere per poterlo seguire senza problemi sono i primi due principi della dinamica di Newton e il calcolo dell'area di un triangolo qualsiasi. I concetti sono quelli usati da Feynman anche se ho cercato di renderli ancora più ... elementari, attraverso molte figure ed esempi.

Il quiz sulla costruzione dell’ellisse era solo un antipasto per una ghiotta e geniale lezione di Richard Feynman. Da Newton a Keplero senza equazioni differenziali e con una matematica e geometria alla portata di tutti coloro che vogliono usare la propria intelligenza e divertirsi, ammirando uno dei più grandi geni al lavoro.

Questo celebre discorso è già stato proposto nel Circolo in versione integrale e in lingua originale. Data la sua importanza e visto che in rete non se ne trova una versione in italiano, per far sì che ogni lettore abbia la possibilità di apprezzarlo, ci siamo rimboccati le maniche e, con grande piacere, lo abbiamo tradotto noi. Buona lettura!

Quelle che seguono sono poche e semplici parole di Richard Feynman, estrapolate dall'introduzione del suo libro "Sei pezzi facili", che il nostro amico Frank ci ha segnalato, reputando che si possano considerare un vero e proprio "manifesto metodologico" di questo Circolo-Blog. Ascoltiamole...