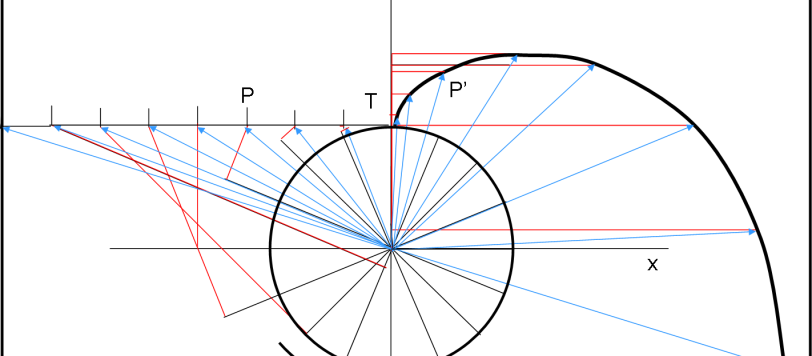
Un problema classico che vale, però, la pena di richiamare: calcolare il punto di caduta di una particella lasciata libera di scivolare su una sfera di raggio R sotto l’effetto della sola gravità terrestre. Un giochino che non è del tutto intuitivo.
Abbiamo visto cosa succederebbe alla Terra se essa decidesse di fermarsi e non girare più attorno al Sole. Potremmo continuare con il nostro pianeta che, però, si è un po' arrabbiato di essere sempre messo in mezzo e allora ci trasferiamo su Papalla che, come sappiamo bene, ha tutte le caratteristiche di massa e di orbita uguali alla Terra. Ma, soprattutto, i papalli sono meno irascibili dei terricoli (tranne uno che - ahimé - conosciamo fin troppo bene e ci tocca sopportarlo perché non se ne vuole più andare!).
Bene, molto bene. Molti hanno risposto e praticamente tutti hanno svolto il quiz correttamente. Tuttavia, data la grande importanza che riveste questo argomento e la tanta confusione che viene spesso fatta in giro per la rete, è meglio ripetere le operazioni da svolgere passo dopo passo in modo da capire non solo la parte “pratica”, ma l’essenza fisica di ciò che andiamo a costruire. Un discorso che deve essere capito da tutti, dato che è veramente un’avventura da seguire con attenzione e senza vere difficoltà. Le considerazioni finali, poi, innescano un nuovo piccolo quiz… Mi raccomando: non snobbate questo articolo, perché è profondamente esplicativo per tutti e ci permette di conoscere sempre meglio le forze fittizie: un argomento veramente fondamentale!
Le risposte sono state più che esaurienti. Tuttavia, può essere utile riassumere le idee ed evitare possibili confusioni tra moto orbitale attorno a Papalla e rotazione di Papalla. Facciamo anche qualche estrapolazione su larga scala. Ricordiamo, comunque, che bloccare istantaneamente la rotazione di un pianeta è un’ipotesi puramente fantascientifica.
Solo un accenno per quei pochi (spero) che rimangono in confusione quando leggono inesattezze molto pesanti e fuorvianti. Gli altri non ci facciano caso…
Per definire e descrivere il momento angolare e le sue proprietà è bene partire fin dall'inizio. Ed ecco che prima di arrivare a lui facciamo la conoscenza dei vettori, delle loro operazioni, della quantità di moto e dei principi della dinamica: una specie di riassunto di gran parte della dinamica classica. Senza dimenticare, ovviamente, la conservazione della quantità di moto e del suo figliolo momento angolare. Per far ciò useremo qualche colpo di scherma, un po' di Divina Commedia, qualche vite e/o qualche mano destra. Infine, mediante l'applicazione del momento angolare a un sistema particolare, introdurremo la dinamica dei moti circolari che imitano quasi perfettamente quelli traslatori o lineari.
Piccoli accenni e tentativi di stimolare, purtroppo, non servono a molto. Valgono molto più l’orgoglio e un po’ di menefreghismo. E allora, seguendo le giuste regole del buon divulgatore (a cui spero sempre più di avvicinarmi) ho scelto la strada più scientifica e produttiva: quella della spiegazione di un concetto che sta facendo cadere sempre più nella confusione e nella paura di azzardare critiche aperte e costruttive. Non mi interessa chi e come ha fatto sorgere la confusione. Il mio compito donchisciottesco è quello ci cercare di proporre una spiegazione più chiara e comprensibile possibile. Niente di più (chissà quando sarò compreso?) e niente di paranoico. Chi ha dubbi li esponga chiaramente. Nel caso potrei anche dire di avere sbagliato tutto. Non sono mai stato e mai sarò un genio come Leonardo o Feynman… Di fronte alla fisica e all’astrofisica sono un semplice studente delle scuole inferiori e devo ancora studiare tanto… Se sbaglio, vi prego, correggetemi!
Vi propongo un esempio lampante di COME non vorrei mai fare divulgazione. Abbiamo finalmente un sito indipendente e sfruttiamolo per far notare, finalmente liberi da catene, il cattivo servizio che viene sovente fatto alla Scienza, girando per i siti dall’apparenza scientifica. Le parole vanno sempre pesate e su di esse bisogna riflettere a lungo. Esse possono fare chiarezza, ma possono anche distruggere anni di lavoro di altri. E questo sia se si è in buona fede (ossia teoricamente preparati) sia che si voglia parlare di cose che non si sanno (ancora più grave).
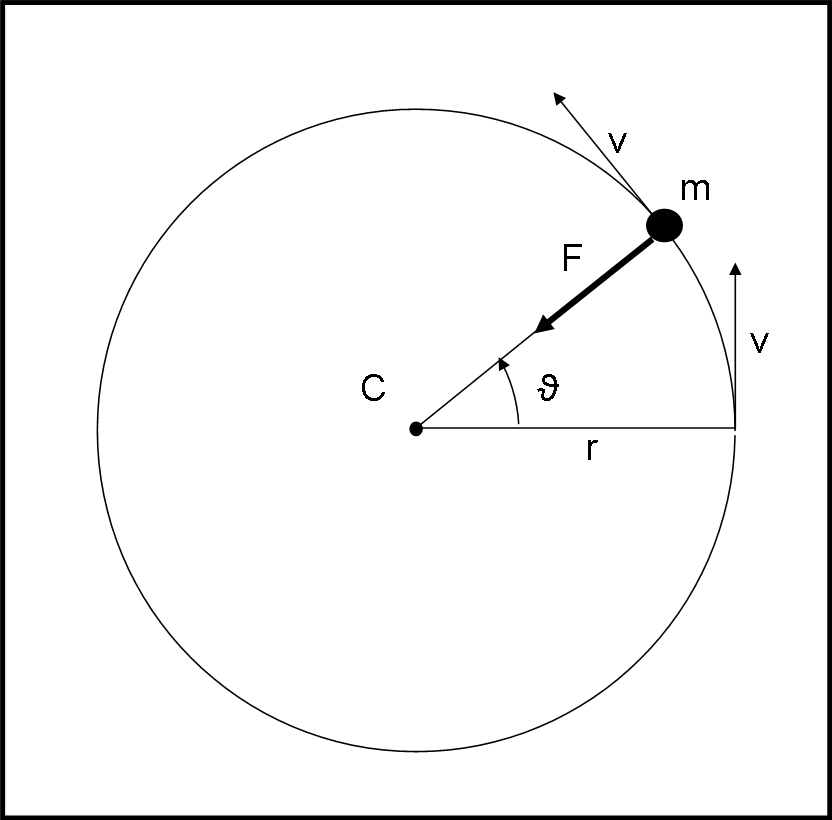
Il problema descritto è quello decisamente importante in fisica, detto del "pendolo conico". Ha risposto solo Alvy (bene)… pazienza… Tuttavia, riporto la soluzione con alcune considerazioni sulla funzione che lega la velocità angolare con l’angolo di apertura della giostra. Aggiungo anche una piccola appendice.
Dopo vari commenti, preferisco scrivere "in bella" la soluzione del Quiz. Ovviamente, l'idea dell'astronauta non era affatto geniale, ma è servita per calcolare il punto di "caduta" di una massa fatta scivolare su una sfera. Verificate il risultato direttamente a casa vostra...
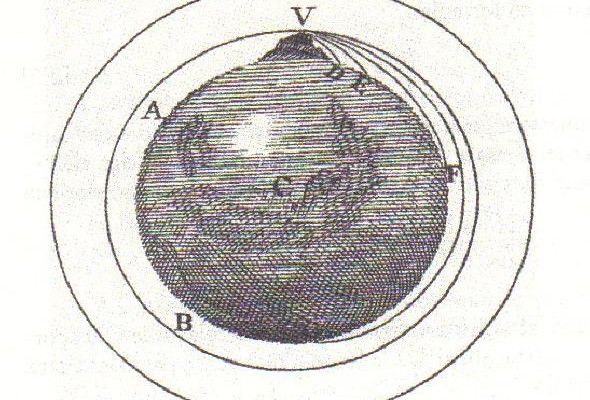
Se io rispondessi di no, qualcuno potrebbe dire che la Luna sta cadendo sulla Terra. Troppo spesso, infatti, si sente dire che la Luna non cade perché la forza centrifuga si oppone a quella centripeta. Purtroppo, c’è molta confusione a riguardo. Non ci resta che utilizzare la Luna per risolvere il problema. In questo articolo si ripassano velocemente i principi della dinamica e non solo. E’, quindi, estremamente sintetico. Ogni frase (anche se ripetuta, come mio solito) va compresa appieno perché definisce, spesso, concetti fondamentali per la comprensione della meccanica classica.