Un apparente paradosso di fisica classica attribuito nientemeno che ad Archimede, che sicuramente avrà utilizzato per uno dei suoi fantastici macchinari.
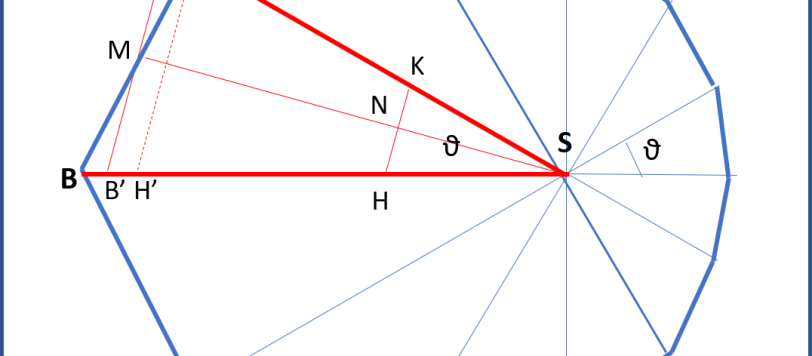
Abbiamo costruito il diagramma delle velocità corrispondente a una traiettoria che segua la seconda legge di Keplero e in cui la forza di attrazione vada con l'inverso della distanza al quadrato. Tuttavia, non sappiamo ancora che traiettoria sia e, soprattutto, non abbiamo ancora dimostrato che il diagramma delle velocità sia proprio un poligono regolare. Iniziamo con quest'ultimo problema.
Un lettore mi ha scritto in privato, sollevando alcuni dubbi sull'articolone sulla forza centrifuga e non solo. Forse è doveroso inserire nuovamente un vecchio articoletto che ne dà una spiegazione estremamente semplice e intuitiva. Sempre in attesa di qualche news veramente interessante...
Abbiamo visto cosa succederebbe alla Terra se essa decidesse di fermarsi e non girare più attorno al Sole. Potremmo continuare con il nostro pianeta che, però, si è un po' arrabbiato di essere sempre messo in mezzo e allora ci trasferiamo su Papalla che, come sappiamo bene, ha tutte le caratteristiche di massa e di orbita uguali alla Terra. Ma, soprattutto, i papalli sono meno irascibili dei terricoli (tranne uno che - ahimé - conosciamo fin troppo bene e ci tocca sopportarlo perché non se ne vuole più andare!).
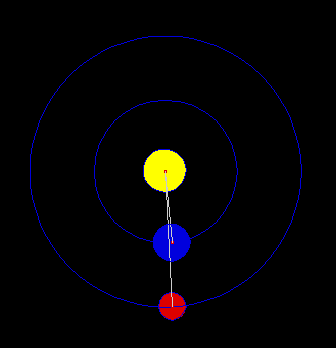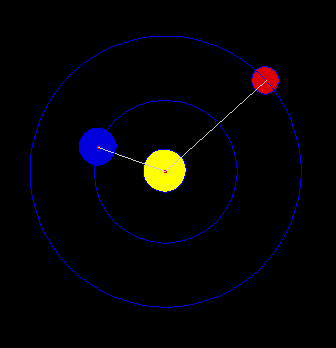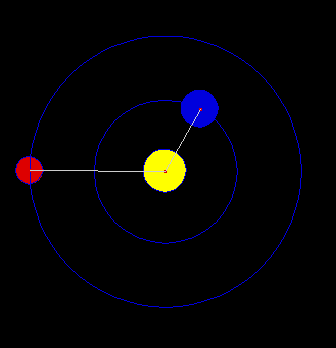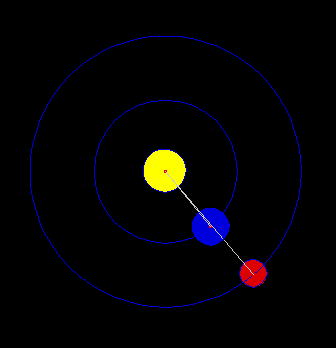
Non ci resta che dedurre la terza legge di Keplero, quella forse più importante e usata. La deduciamo per un’orbita qualsiasi, ma è già ben noto (e immediato) il procedimento da usare nel caso di un’orbita circolare, che richiamiamo per semplicità.
Solo un accenno per quei pochi (spero) che rimangono in confusione quando leggono inesattezze molto pesanti e fuorvianti. Gli altri non ci facciano caso…
Piccoli accenni e tentativi di stimolare, purtroppo, non servono a molto. Valgono molto più l’orgoglio e un po’ di menefreghismo. E allora, seguendo le giuste regole del buon divulgatore (a cui spero sempre più di avvicinarmi) ho scelto la strada più scientifica e produttiva: quella della spiegazione di un concetto che sta facendo cadere sempre più nella confusione e nella paura di azzardare critiche aperte e costruttive. Non mi interessa chi e come ha fatto sorgere la confusione. Il mio compito donchisciottesco è quello ci cercare di proporre una spiegazione più chiara e comprensibile possibile. Niente di più (chissà quando sarò compreso?) e niente di paranoico. Chi ha dubbi li esponga chiaramente. Nel caso potrei anche dire di avere sbagliato tutto. Non sono mai stato e mai sarò un genio come Leonardo o Feynman… Di fronte alla fisica e all’astrofisica sono un semplice studente delle scuole inferiori e devo ancora studiare tanto… Se sbaglio, vi prego, correggetemi!
Vi propongo un esempio lampante di COME non vorrei mai fare divulgazione. Abbiamo finalmente un sito indipendente e sfruttiamolo per far notare, finalmente liberi da catene, il cattivo servizio che viene sovente fatto alla Scienza, girando per i siti dall’apparenza scientifica. Le parole vanno sempre pesate e su di esse bisogna riflettere a lungo. Esse possono fare chiarezza, ma possono anche distruggere anni di lavoro di altri. E questo sia se si è in buona fede (ossia teoricamente preparati) sia che si voglia parlare di cose che non si sanno (ancora più grave).
Il problema descritto è quello decisamente importante in fisica, detto del "pendolo conico". Ha risposto solo Alvy (bene)… pazienza… Tuttavia, riporto la soluzione con alcune considerazioni sulla funzione che lega la velocità angolare con l’angolo di apertura della giostra. Aggiungo anche una piccola appendice.
Piccola aggiunta per i più bravi e per chi non se la sente di partire dalla superficie...
Abbiamo trovato la forza di marea in tanti luoghi dell'Universo: dalle galassie, ai buchi neri, agli oceani terrestri, fino ai piccoli asteroidi che si avvicinano troppo a un pianeta. Sembra agire in modo diverso, ma è sempre la stessa. Penso di fare cosa gradita a molti nel voler riunire vari articoli e descrivere sia come si determina sia come agisce. Un solo asterisco per chi vuole limitarsi ai concetti, tre per chi vuole seguire anche i calcoli.