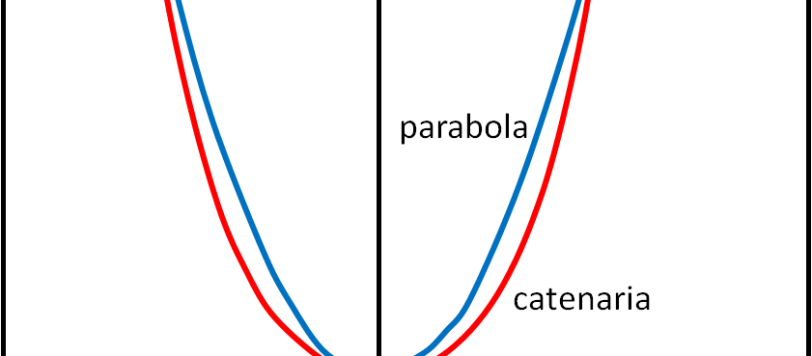
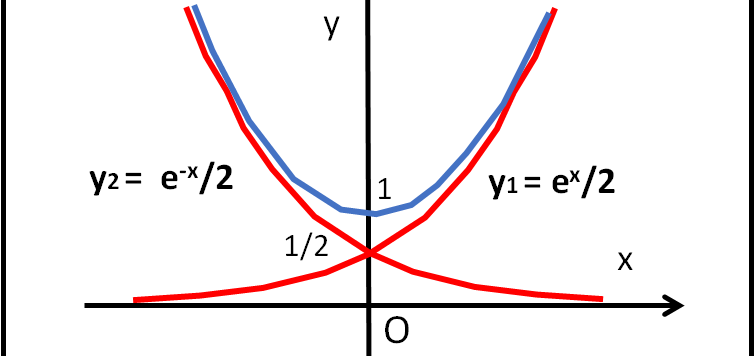
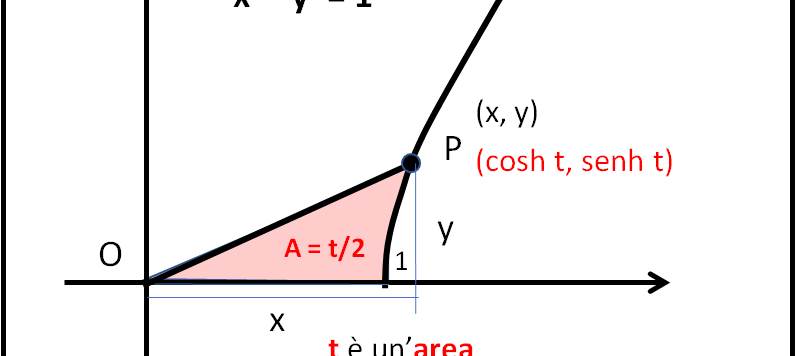
Affrontiamo lo scoglio maggiore di questa serie di articoli, ossia determiniamo l'equazione della catenaria, quella "strana" condizione di equilibrio di una catenella sospesa tra due chiodi intorno alla quale Galileo ha disquisito, accorgendosi di non essere in grado di ricavarla e accontentandosi di approssimarla a una parabola.
Prima di affrontare la determinazione analitica della curva oggi chiamata catenaria, ricordiamo come essa sia stata trattata da Galileo Galilei nei suoi Discorsi su due Nuove Scienze, senza che il grande pisano trovasse una descrizione definitiva.
Verifichiamo ancora una volta il significato delle funzioni iperboliche e vediamo che forma hanno. In fondo, è proprio questa forma che ci verrà utile in seguito, anche per comprendere le argomentazioni di Galileo Galilei.
In questa sezione vogliamo dimostrare come le funzioni iperboliche possano anche essere definite attraverso la partecipazione attiva del numero e. Nel contempo vogliamo anche mostrare la relazione che esiste tra funzioni trigonometriche classiche e le funzioni iperboliche. Per fare ciò è fondamentale utilizzare la formula di Eulero, proprio quella che ha portato, come caso particolare, alla sua celeberrima identità, di cui abbiamo già parlato.
Iniziamo il nostro lungo percorso verso i ponti sospesi partendo da lontano. In particolare, dalle funzioni trigonometriche che conosciamo tutti molto bene.