Questo problemino è estremamente interessante in quanto ci fa ragionare su un caso molto realistico di pura geometria non euclidea, ma che presenta dei risvolti che vanno ben oltre. Non vi dico quali, altrimenti vi aiuterei troppo nella soluzione.
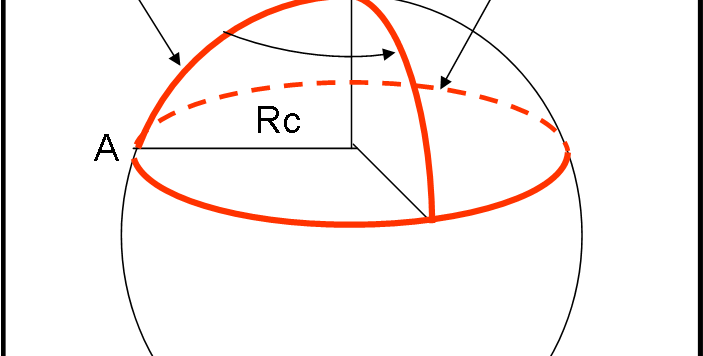
Questo articolo non contiene praticamente formule, ma è decisamente FONDAMENTALE per capire l’essenza più profonda della RG e della sua definizione di spazio tridimensionale curvo. Non perdetelo e non esitate a porre domande se vi rimane qualche dubbio. Capirete anche perché abbiamo perso tanto tempo a spiegare le regole geometriche di una superficie sferica, confrontandole con quelle euclidee e anche perché abbiamo scaldato un piano con una strana piastra. Sembrerà una trattazione addirittura pedante, ma il concetto di curvatura è troppo importante per rischiare di non chiarirlo completamente.
Questo lungo articolo riunisce tutti quelli relativi alla geometria sferica. Esso è stato anche inserito tra gli approfondimenti.
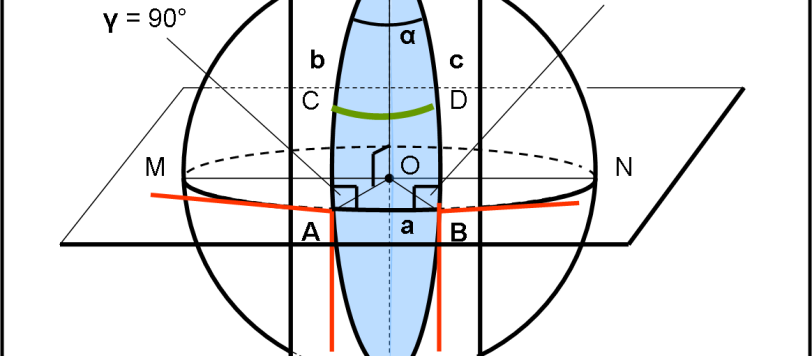
Definiti i lati di un triangolo sferico, non ci resta che definire quali siano i suoi angoli. Nel fare questo, risolviamo il vecchio quiz e stabiliamo anche un’altra proprietà molto interessante dei triangoli sferici. Concludiamo con due nuovi quiz, che saranno risolti la volta successiva.
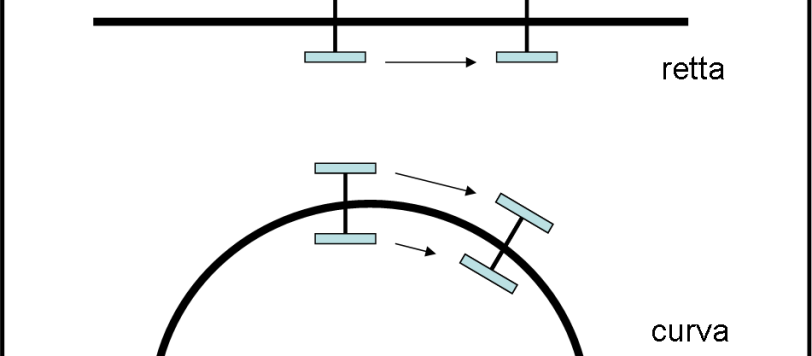
Iniziamo la nostra vita su una superficie sferica, obbligandoci a ragionare e a definire la geometria su di essa senza sfruttare la nostra capacità di osservare nelle tre dimensioni. Un impegno non sempre immediato, ma che deve essere affrontato per capire perfettamente una geometria non euclidea, la geometria che governa la sfera celeste (e anche la superficie terrestre), ma non solo. Ripeteremo, poi, gli stessi concetti usando una visione estrinseca, decisamente più comoda, ma i due metodi usati per giungere alla stessa meta daranno un quadro veramente completo della situazione
Questo articolo vuole essere l’introduzione alla geometria sferica, che ci permetterà di descrivere il cielo stellato e le coordinate celesti. Tuttavia, è anche il primo passo verso uno spazio e addirittura uno spaziotempo curvo, base fondamentale per affrontare la Relatività Generale. Non perdetevi, perciò, le varie puntate…
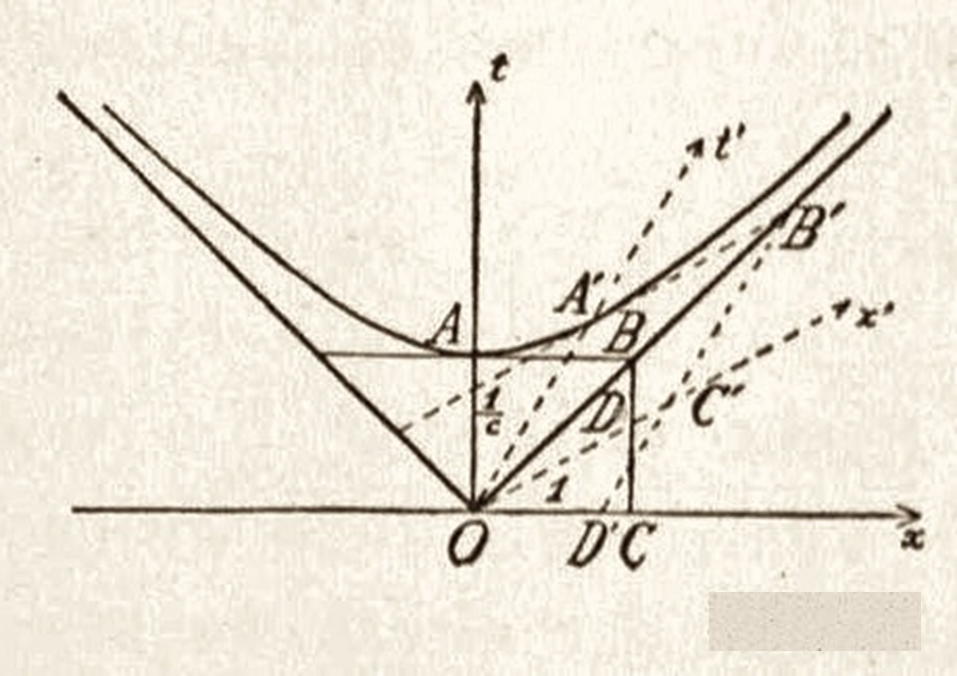
Questo quarto articolo conclude in qualche modo la presentazione del diagramma di Minkowski da un punto di vista puramente geometrico. Viene introdotto l’invariante spaziotemporale e si capisce molto meglio cosa rappresentano le iperboli trovate precedentemente. La dilatazione dei tempi segue quasi automaticamente. Tuttavia, ci fermiamo un attimo prima. L’articolo può risultare un po’ difficile se non si legge con grande attenzione e non si collega continuamente con quelli precedenti. Lo lasciamo un bel po’ in visione in attesa di domande e dubbi riguardanti “solo” lui. Mi raccomando, non cerchiamo di estrapolare in avanti se no si rischia veramente di confondere i meno preparati. Lo scopo ultimo deve essere quello di regalare a TUTTI la RR e non provare la capacità di pochi…