Quest'articolo tenta una dimostrazione geometrica unitaria della complanarità e non complanarità delle facce di solidi semplice come il tetraedro e la piramide. Lo fa attraverso le proiezioni e devo dire che la visione delle varie figure non è proprio banale, da cui i tre asterischi.
In questo articolo descrivo la realizzazione di un modello di geometria solida con il quale ho voluto verificare il funzionamento di una montatura equatoriale, ossia un particolare sostegno di un telescopio molto utilizzato in ambito amatoriale e non solo. La montatura equatoriale consente con un unico movimento, manuale o motorizzato, di "inseguire" il moto apparente di un astro nel cielo, in realtà ruotando in sincrono col moto di rotazione terrestre.
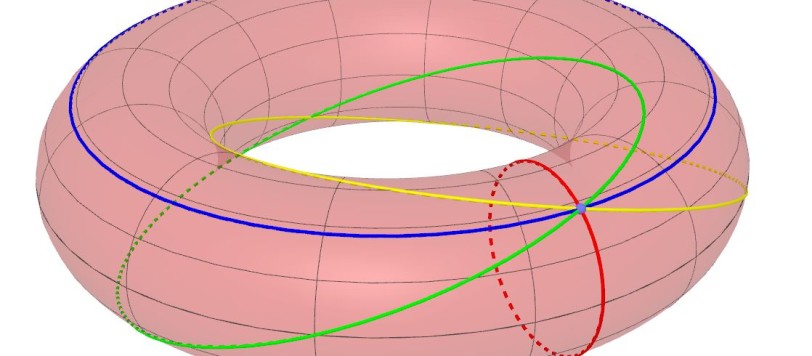
Rieccoci qui con l'ultima parte dell'appendice all'articolo 8° sulla geometria solida, dedicato al toro. Nella prima appendice abbiamo fatto la conoscenza delle circonferenze di Villarceau. In questa seconda appendice illustrerò altre interessanti curve ottenibili andando a sezionare il toro con un particolare piano. Ci serviremo, come sempre in geometria analitica dello spazio, del linguaggio della matematica. Ma niente paura, useremo strumenti semplici. E, in ogni caso, se avete dubbi, non avete che da chiedere nei commenti.
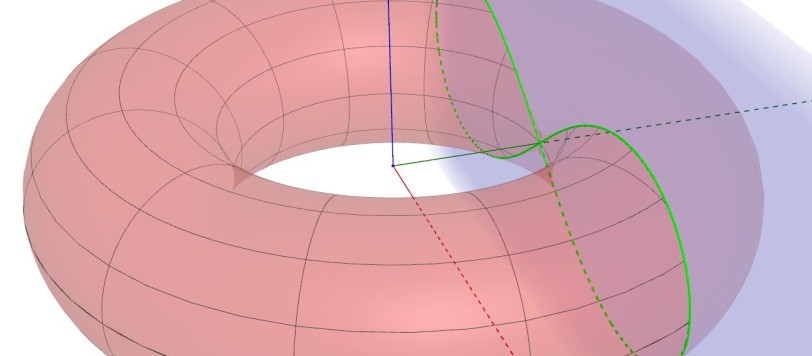
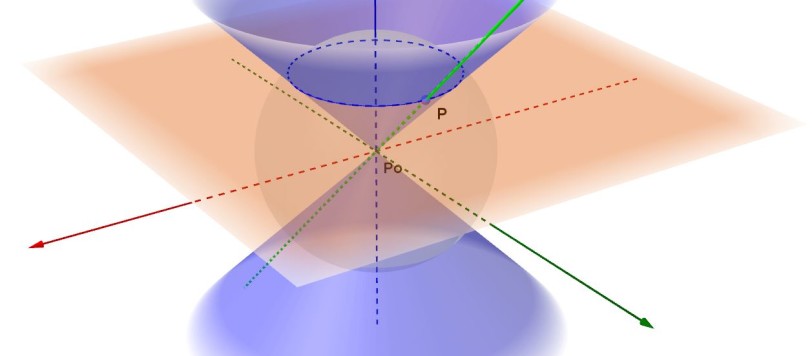
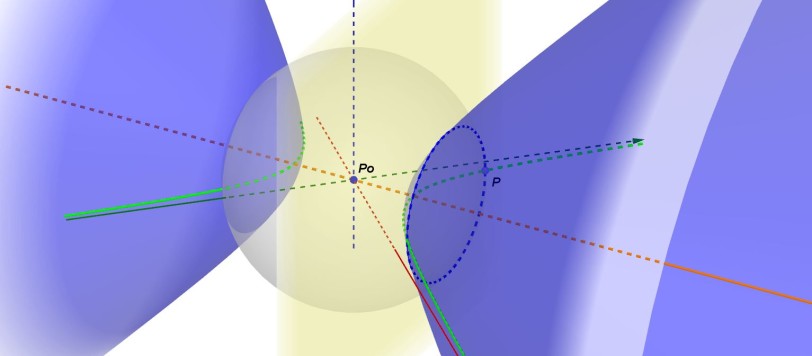
L'ultima volta avevo concluso l'articolo accennando alle sezioni spiriche, che sono proprio quelle di cui ci occupiamo questa volta. Intanto, perché si chiamano spiriche ?
In questa appendice all'articolo sul toro analizzeremo le curve risultanti dalla sezione del toro con determinati piani secanti. Scopriremo le bellissime circonferenze di Villarceau, l'ippopede di Proclo , gli ovali di Cassini, le lemniscate di Booth e di Bernoulli. Vedremo come la geometria solida sa regalarci momenti di autentica meraviglia. L'appendice è divisa in due parti. La prima è dedicata alle sole circonferenze di Villarceu.
Nell'ultima nostra chiacchierata sulle superfici di rotazione ci eravamo lasciati con l'intesa che nella successiva avremmo fatto la conoscenza di una superficie di rotazione che ricorda tanto una ciambella. Eccoci , dunque, qui a parlare del "toro" o "toroide"
In questo articolo della serie dedicata alle superfici di rotazione ricaviamo la rappresentazione analitica di iperboloidi di rotazione a una falda e a due falde. Possibilità di visualizzare i relativi modelli geometrici, anche in 3D.
Nel mio precedente articolo ho cercato di spiegare cosa siano in geometria dello spazio le superfici di rotazione e un metodo per determinarne la rappresentazione analitica. In questo articolo fornirò una prima serie di esempi, più semplici, utilizzando ancora la possibilità di visualizzazione tridimensionale anche attraverso l'uso di occhiali anaglifici. Rammento per comodità che una […]
In questo articolo faremo la conoscenza di una particolare entità geometrica spaziale che ritroviamo in molti esempi della realtà che ci circonda: la superficie di rotazione. Vedremo, inoltre, come ricavarne la rappresentazione analitica. Come si intuisce dal suo stesso nome, tale entità geometrica è generata dalla rotazione di una curva attorno ad una retta, detta […]